
分析 通过3Sn=4n+1-4与3Sn-1=4n-4(n-2)作差,进而计算可知an=4n,利用错位相减法计算即得结论.
解答 解:∵3Sn=4n+1-4,
∴3Sn-1=4n-4(n-2)(n≥2),
两式相减得:3an=3×4n,即an=4n(n≥2),
又∵3S1=41+1-4,即a1=4满足上式,
∴an=4n,
记数列{(3n-2)an}的前n项和为Tn,则:
Tn=1×4+4×42+…+(3n-2)×4n,
4Tn=1×42+4×43+…+(3n-5)×4n+(3n-2)×4n+1,
两式相减得:-3Tn=4+3(42+43+…+4n)-(3n-2)×4n+1
=4+3×$\frac{{4}^{2}(1-{4}^{n-1})}{1-4}$-(3n-2)×4n+1
=4+4n+1-16-(3n-2)×4n+1
=-(3n-3)×4n+1-12,
∴Tn=4+(n-1)×4n+1,
故答案为:4+(n-1)×4n+1.
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,足球门框的长AB为2dw(1dw=3.66m),设足球为一点P,足球与A,B连线所成的角为α(0°<α<90°).
如图,足球门框的长AB为2dw(1dw=3.66m),设足球为一点P,足球与A,B连线所成的角为α(0°<α<90°).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
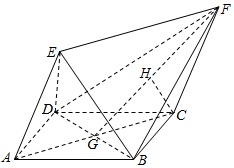 四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点,AB=BD=2,AE=$\sqrt{3}$,CH=$\frac{{\sqrt{3}}}{2}$.
四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点,AB=BD=2,AE=$\sqrt{3}$,CH=$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com