
分析 先根据分组分配求出3首歌都有班级选择的种数,再求出任选一首歌的种数,根据概率公式计算即可.
解答 解:5个班可以都分为(3,1,1)和(2,2,1)两组,
第一类(3,1,1)有C53=10种,
第二类(2,2,1)有$\frac{{C}_{5}^{2}{C}_{3}^{2}{C}_{1}^{1}}{{A}_{2}^{2}}$=15种,
共有10+15=25种分组方法,
则3首歌都有班级选择为25A33=150,
高二年级5个班,每个班只能在《Nobody》,《suger》,《Catch Me》3首歌中任意选择一首作为自编操曲目,共有35=243种,
故则3首歌都有班级选择的概率为$\frac{150}{243}$=$\frac{50}{81}$
故答案为:$\frac{50}{81}$
点评 本题考查了排列组合和古典概率的问题,关键是分组分配,属于中档题.


科目:高中数学 来源: 题型:解答题
 已知如图,△ABC和△DBC所在的平面互相垂直,且AB=BC=BD=1,∠ABC=∠DBC=120°.
已知如图,△ABC和△DBC所在的平面互相垂直,且AB=BC=BD=1,∠ABC=∠DBC=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题①成立,命题②不成立 | B. | 命题①不成立,命题②成立 | ||
| C. | 命题①和命题②都成立 | D. | 命题①和命题②都不成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
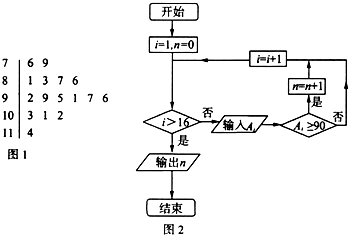 图1是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次是A1,A2,…,A16,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )
图1是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次是A1,A2,…,A16,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )| A. | 6 | B. | 7 | C. | 10 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com