
分析 (Ⅰ)由题意可得,F1F2=PF2,即(a-c)2+b2=4c2,再由${S}_{△P{F}_{1}{F}_{2}}=\sqrt{3}$,得bc=$\sqrt{3}$,然后结合隐含条件求得a,b,则椭圆方程可求;
(Ⅱ)(i)由$\overrightarrow{Q{F}_{1}}=λ\overrightarrow{MN}$,得则QF1⊥x轴,由(Ⅰ)求得F1(-1,0),设Q(-1,y),代入椭圆方程即可求得Q坐标;
(ii)设Q(x0,y0),得直线QA方程为$y=\frac{{y}_{0}}{{x}_{0}+2}(x+2)$,求出M点的坐标为(m,$\frac{(m+2){y}_{0}}{{x}_{0}+2}$).同理得N的坐标为$(m,\frac{(m-2){y}_{0}}{{x}_{0}-2})$.由${k}_{M{F}_{1}}•{k}_{N{F}_{1}}$=-1求得m=-4.可知存在实数m=-4,使得以MN为直径的圆经过点F.
解答 解:(Ⅰ)F1(-c,0),F2(c,0),由题意可得,F1F2=PF2,
∴(a-c)2+b2=4c2,
由${S}_{△P{F}_{1}{F}_{2}}=\sqrt{3}$,可得$\frac{1}{2}•2c•b=bc=\sqrt{3}$,
又a2=b2+c2,联立可得a=2,b=$\sqrt{3}$,
∴椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)(i)∵$\overrightarrow{Q{F}_{1}}=λ\overrightarrow{MN}$,
∴QF1∥MN,则QF1⊥x轴,
由(Ⅰ)知,c2=1,则F1(-1,0),
设Q(-1,y),则有$\frac{1}{4}+\frac{{y}^{2}}{3}=1$,即y=$±\frac{3}{2}$,
∴Q(-1,$±\frac{3}{2}$);
(ii)设Q(x0,y0),则${k}_{QA}=\frac{{y}_{0}}{{x}_{0}+2}$,直线QA方程为$y=\frac{{y}_{0}}{{x}_{0}+2}(x+2)$,
令x=m,得M点的坐标为(m,$\frac{(m+2){y}_{0}}{{x}_{0}+2}$).
同理${k}_{QB}=\frac{{y}_{0}}{{x}_{0}-2}$,直线QB的方程为$y=\frac{{y}_{0}}{{x}_{0}-2}(x-2)$,
得N的坐标为$(m,\frac{(m-2){y}_{0}}{{x}_{0}-2})$.
∴${k}_{M{F}_{1}}•{k}_{N{F}_{1}}=\frac{\frac{(m+2){y}_{0}}{2+{x}_{0}}}{m+1}•\frac{\frac{(m-2){y}_{0}}{{x}_{0}-2}}{m+1}$=$\frac{({m}^{2}-4){{y}_{0}}^{2}}{(m+1)^{2}({{x}_{0}}^{2}-4)}$.
又Q(x0,y0)在椭圆上,
∴$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{3}=1$,则$\frac{{{y}_{0}}^{2}}{{{x}_{0}}^{2}-4}=-\frac{3}{4}$.
∴${k}_{M{F}_{1}}•{k}_{N{F}_{1}}$=$\frac{{m}^{2}-4}{(m+1)^{2}}•(-\frac{3}{4})=-1$.
解得m=-4.
∴存在实数m=-4,使得以MN为直径的圆经过点F.
点评 本题考查椭圆的标准方程,考查了椭圆的简单性质,考查直线与圆锥曲线位置关系的应用,考查逻辑思维能力及运算求解能力,属难题.


科目:高中数学 来源: 题型:解答题
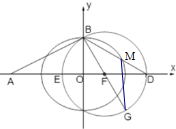 如图,已知F(c,0)是椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的右焦点;圆F:(x-c)2+y2=a2与x轴交于D,E两点,其中E是椭圆C的左焦点.
如图,已知F(c,0)是椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的右焦点;圆F:(x-c)2+y2=a2与x轴交于D,E两点,其中E是椭圆C的左焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知如图,△ABC和△DBC所在的平面互相垂直,且AB=BC=BD=1,∠ABC=∠DBC=120°.
已知如图,△ABC和△DBC所在的平面互相垂直,且AB=BC=BD=1,∠ABC=∠DBC=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题①成立,命题②不成立 | B. | 命题①不成立,命题②成立 | ||
| C. | 命题①和命题②都成立 | D. | 命题①和命题②都不成立 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com