
分析 (1)甲不在排头,也不在排尾,先选2人排在排头和排尾,其他人任意排,问题得以解决;
(2)甲、乙、丙三人必须在一起,先把甲乙丙三人捆绑在一起,再和另外6人全排,问题得以解决;,
(3)甲、乙、丙三人两两不相邻,先排除甲乙丙之外的6人,形成了7个空,把甲乙丙插入,问题得以解决;,
(4)甲不排头,乙不排当中,利用间接法
解答 解:(1)甲不在排头,也不在排尾,先选2人排在排头和排尾,其他人任意排,故有A82A77=282240种,
(2)甲、乙、丙三人必须在一起,先把甲乙丙三人捆绑在一起,再和另外6人全排,故有A33A77=5040种,
(3)甲、乙、丙三人两两不相邻,先排除甲乙丙之外的6人,形成了7个空,把甲乙丙插入,故有A33A77=5040种,
(4)不考虑限制条件有A99,而甲排头有A88,乙排当中有A88,这样重复了甲排头,乙排当中A77次,即A99-2A88+A77=47880种.
点评 本题考查排列、组合的应用,注意特殊问题的处理方法,如相邻用捆绑法,不能相邻用插空法,属于中档题.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
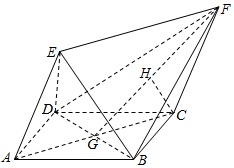 四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点,AB=BD=2,AE=$\sqrt{3}$,CH=$\frac{{\sqrt{3}}}{2}$.
四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点,AB=BD=2,AE=$\sqrt{3}$,CH=$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2013 | C. | 2014 | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com