
分析 (Ⅰ)运用椭圆的定义可得a=2,由离心率公式可得c,再由a,b,c的关系可得b,进而得到椭圆方程;
(Ⅱ)设点P(x1,y1),Q(x2,y2),联立直线方程和椭圆方程,消去y,可得x的方程,运用韦达定理和等比数列的中项的性质,化简整理可得k,m的关系;
(III)设点O到直线PQ的距离为d,运用点到直线的距离公式,以及弦长公式,三角形的面积公式,化简整理点到m的式子,再由基本不等式即可得到最大值,检验,进而得到所求范围.
解答 解:(Ⅰ)由椭圆的定义可得|PF1|+|PF2|=2a=4,可得a=2,
由e=$\frac{c}{a}$=$\frac{{\sqrt{3}}}{2}$,可得c=$\sqrt{3}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
则椭圆方程为$\frac{x^2}{4}+{y^2}=1$;
(Ⅱ)设点P(x1,y1),Q(x2,y2),
由$\left\{\begin{array}{l}y=kx+m\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$,消y,得(4k2+1)x2+8kmx+4m2-4=0,
因为直线与椭圆交于不同的两点,
所以△=64k2m2-16(m2-1)(4k2+1)>0,
解得4k2+1>m2,
由韦达定理得,${x_1}+{x_2}=-\frac{8km}{{4{k^2}+1}}$,${x_1}{x_2}=\frac{{4{m^2}-4}}{{4{k^2}+1}}$,
由题意知,k2=kOP•kOQ,
即${k^2}=\frac{{{y_1}{y_2}}}{{{x_1}{x_2}}}=\frac{{{k^2}{x_1}{x_2}+km({x_1}+{x_2})+{m^2}}}{{{x_1}{x_2}}}={k^2}+\frac{{km({x_1}+{x_2})}}{{{x_1}{x_2}}}+\frac{m^2}{{{x_1}{x_2}}}$,
即为$\frac{{km({x_1}+{x_2})}}{{{x_1}{x_2}}}+\frac{m^2}{{{x_1}{x_2}}}=0$,
即有-$\frac{8{k}^{2}{m}^{2}}{1+4{k}^{2}}$+m2=0,
即${k^2}=\frac{1}{4}$,即k=±$\frac{1}{2}$,0<m2<2;
(III)设点O到直线PQ的距离为d,
则$d=\frac{|m|}{{\sqrt{1+{k^2}}}}$,$|{PQ}|=\sqrt{{{({{x_1}-{x_2}})}^2}+{{({{y_1}-y_2^{\;}})}^2}}$=$\sqrt{1+{k^2}}$$\frac{{\sqrt{△}}}{{1+4{k^2}}}$
=4$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{1+4{k}^{2}-{m}^{2}}}{1+4{k}^{2}}$,
由(Ⅱ)可得1+4k2=2,
所以${S_{△OPQ}}=\frac{1}{2}|{PQ}|d=|m|\sqrt{2-{m^2}}$,
则${S^2}_{△OPQ}={m^2}({2-{m^2}})$≤$\frac{{m}^{2}+2-{m}^{2}}{2}$=1,
由m2=1时,k=0,仅有一个交点,则最大值1取不到.
则△OPQ面积的取值范围是(0,1).
点评 本题考查椭圆的方程的求法,注意运用椭圆的定义和离心率公式,考查直线方程和椭圆方程联立,运用韦达定理,以及等比数列的中项的性质和直线的斜率公式,同时考查三角形的面积的范围,注意运用弦长公式和点到直线的距离公式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
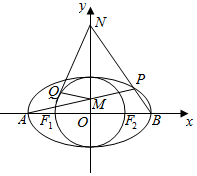 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上的点到它的两个焦点的距离之和为4,以椭圆C的短轴为直径的圆O经过两个焦点,A,B是椭圆C的长轴端点.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上的点到它的两个焦点的距离之和为4,以椭圆C的短轴为直径的圆O经过两个焦点,A,B是椭圆C的长轴端点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
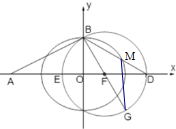 如图,已知F(c,0)是椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的右焦点;圆F:(x-c)2+y2=a2与x轴交于D,E两点,其中E是椭圆C的左焦点.
如图,已知F(c,0)是椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的右焦点;圆F:(x-c)2+y2=a2与x轴交于D,E两点,其中E是椭圆C的左焦点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
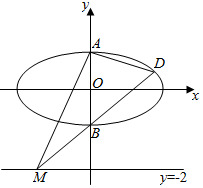 已知椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{b^2}$=1(2>b>0)的上、下顶点分别为A、B,过点B的直线与椭圆交于另一点D,与直线y=-2交于点M.
已知椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{b^2}$=1(2>b>0)的上、下顶点分别为A、B,过点B的直线与椭圆交于另一点D,与直线y=-2交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆M:$\frac{{x}^{2}}{2{c}^{2}}$+$\frac{{y}^{2}}{{c}^{2}}$=1(c>0)的离心率为e,右焦点为(c,0).
已知椭圆M:$\frac{{x}^{2}}{2{c}^{2}}$+$\frac{{y}^{2}}{{c}^{2}}$=1(c>0)的离心率为e,右焦点为(c,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com