
���� �ٸ������洹ֱ�����洹ֱ�����ʽ����жϣ�
�ڸ�����ѧ���ɷ��Ķ�������жϣ�
�۸�����������Ķ�������жϣ�
�ܸ������ָ��R2�����ʽ����жϣ�
�ݸ��ݿռ��ĶԳ��Խ����жϣ�
��� �⣺����ֱ֪��m��n��ƽ������£���n�ͦ£����ͦ£���n�Φ���n?ƽ�������m�Φ�����m��n��m��n�ཻ��m��n������ֱ�ߣ��ʢٴ���
������ѧ���ɷ�֤����n+1����n+2������n+n��=2n•1•3����2n+1����n��N*������n=k��n=k+1ʱ��
��n=k+1ʱ����k+1+1����k+1+2������k+1+k+1��=��k+2����k+3������2k+2�������ʽ�����˵Ĵ���ʽ�ǣ�2k+1����2k+2��•$\frac{1}{k+1}$���ʢڴ���
�۶����⡰����������������Բ���������е㡱����Ȳ��룺���������������������ڸ������ģ�������������Ķ��壬�ʢ���ȷ��
�����ж���������y��x�Ƿ����ʱ��ѡ����3����ͬ��ģ�ͣ����ǵ����ָ��R2�ֱ�Ϊ��ģ��1Ϊ0.98��ģ��2Ϊ0.80��ģ��3Ϊ0.50���������Ч����õ���ģ��1��
��ȷ������R2Խ�������Ч����ã��ʢ���ȷ��
���ڿռ�ֱ������ϵ�У���A��1��2��1������y��ĶԳƵ�A�������Ϊ��-1��2��-1������ȷ������y��Գ���y���䣬���������෴���ʢ���ȷ��
�ʴ�Ϊ���ۢܢ�
���� ������Ҫ�������������жϣ��漰��֪ʶ��϶࣬�ۺ��Խ�ǿ�����ѶȲ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
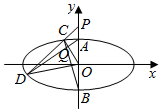 ��ԲM��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2����P��0��2������ֱ��y=-x�ĶԳƵ�����ԲM�ϣ���|F1F2|=2$\sqrt{3}$
��ԲM��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2����P��0��2������ֱ��y=-x�ĶԳƵ�����ԲM�ϣ���|F1F2|=2$\sqrt{3}$�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
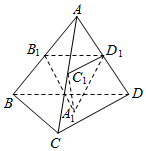 ��ͼ����������ABCD�У���B1��C1��D1�ֱ�����AB��AC��AD�ϣ���ƽ��B1C1D1��ƽ��BCD��A1Ϊ��BCD��һ�㣬������A1-B1C1D1�����ΪV����$\frac{{A{D_1}}}{AD}=x$�����ں���V=F��x����������ѡ����ȷ���ǣ�������
��ͼ����������ABCD�У���B1��C1��D1�ֱ�����AB��AC��AD�ϣ���ƽ��B1C1D1��ƽ��BCD��A1Ϊ��BCD��һ�㣬������A1-B1C1D1�����ΪV����$\frac{{A{D_1}}}{AD}=x$�����ں���V=F��x����������ѡ����ȷ���ǣ�������| A�� | ����F��x����$��{\frac{1}{2}��1}��$���Ǽ����� | |
| B�� | ����F��x����ͼ�����ֱ��$x=\frac{1}{2}$�Գ� | |
| C�� | ��$x=\frac{2}{3}$ʱ������F��x��ȡ�����ֵ | |
| D�� | ����x0��ʹ��$F��{x_0}����\frac{7}{27}{V_{A-BCD}}$������VA-BCDΪ������ABCD������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com