
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据等比数列的定义进行判断,
②根据向量数量积的公式进行判断,
③根据向量数量积的应用进行判断,
④根据三角函数的图象和性质,利用辅助角公式进行化简进行判断.
解答 解:①非零的常数数列一定是等比数列,当零常数列不是等比数列,故①错误;
②在△ABC中,若$\overrightarrow{AB}$•$\overrightarrow{BC}$>0,则|$\overrightarrow{AB}$|•|$\overrightarrow{BC}$|cos(π-B)>0,即-cosB>0,则cosB<0.则B是钝角,则△ABC是钝角三角形,故②错误;
③若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则平方得$\overrightarrow{a}$2+$\overrightarrow{b}$2+$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$2+$\overrightarrow{b}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$,则$\overrightarrow{a}$•$\overrightarrow{b}$,即$\overrightarrow{a}$⊥$\overrightarrow{b}$成立,故③正确;
④若f(x)=sin2x+sinxcosx,则f(x)=$\frac{1}{2}$-$\frac{1}{2}$cos2x+$\frac{1}{2}$sin2x=$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$),
由2x-$\frac{π}{4}$=kπ+$\frac{π}{2}$得x=$\frac{4k+3π}{8}$,
当k=-1时,x=-$\frac{π}{8}$,即函数f(x)的图象关于直线x=-$\frac{π}{8}$对称.正确,故④正确,
故选:B
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但难度不大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 60种 | B. | 30种 | C. | 25种 | D. | 20种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
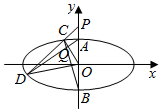 椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,点P(0,2)关于直线y=-x的对称点在椭圆M上,且|F1F2|=2$\sqrt{3}$
椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,点P(0,2)关于直线y=-x的对称点在椭圆M上,且|F1F2|=2$\sqrt{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
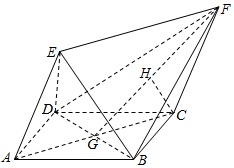 四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点,AB=BD=2,AE=$\sqrt{3}$,CH=$\frac{{\sqrt{3}}}{2}$.
四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点,AB=BD=2,AE=$\sqrt{3}$,CH=$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com