
分析 (Ⅰ)由椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,直线l:x-my-1=0(m∈R)过椭圆C的右焦点F,列出方程组,求出a,b,由此能求出椭圆C的标准方程.
(Ⅱ)令m=0,则A(1,$\frac{3}{2}$),B(1,-$\frac{3}{2}$)或A(1,-$\frac{3}{2}$),B(1,$\frac{3}{2}$),从而得到满足题意的定点只能是($\frac{5}{2}$,0),设为D点,再证明P、B、D三点共线.由此得到BP恒过定点($\frac{5}{2}$,0).
解答 解:(Ⅰ)∵椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,直线l:x-my-1=0(m∈R)过椭圆C的右焦点F,
∴由题设,得$\left\{\begin{array}{l}{c=1}\\{\frac{c}{a}=\frac{1}{2}}\end{array}\right.$,
解得a=2,c=1,∴b2=a2-c2=3,
∴椭圆C的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(Ⅱ)令m=0,则A(1,$\frac{3}{2}$),B(1,-$\frac{3}{2}$)或A(1,-$\frac{3}{2}$),B(1,$\frac{3}{2}$),
当A(1,$\frac{3}{2}$),B(1,-$\frac{3}{2}$)时,P(4,$\frac{3}{2}$),直线BP:y=x-$\frac{5}{2}$,
当A(1,-$\frac{3}{2}$),B(1,$\frac{3}{2}$)时,P(4,-$\frac{3}{2}$),直线BP:y=-x+$\frac{5}{2}$,
∴满足题意的定点只能是($\frac{5}{2}$,0),设为D点,下面证明P、B、D三点共线.
设A(x1,y1),B(x2,y2),
∵PA垂直于y轴,∴点P的纵坐标为y1,从而只要证明P(4,y1)在直线BD上,
由$\left\{\begin{array}{l}{x-my-1=0}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(4+3m2)y2+6my-9=0,
∵△=144(1+m2)>0,∴${y}_{1}+{y}_{2}=\frac{-6m}{4+3{m}^{2}}$,${y}_{1}{y}_{2}=\frac{-9}{4+3{m}^{2}}$,①
∵kDB-kDP=$\frac{{y}_{2}-0}{{x}_{2}-\frac{5}{2}}$-$\frac{{y}_{1}-0}{4-\frac{5}{2}}$=$\frac{{y}_{2}}{m{y}_{2}+1-\frac{5}{2}}$-$\frac{{y}_{1}}{\frac{3}{2}}$=$\frac{\frac{3}{2}{y}_{2}-{y}_{1}(m{y}_{2}-\frac{3}{2})}{\frac{3}{2}(m{y}_{2}-\frac{3}{2})}$=$\frac{{y}_{1}+{y}_{2}-\frac{2}{3}m{y}_{1}{y}_{2}}{m{y}_{2}-\frac{3}{2}}$,
①式代入上式,得kDB-kDP=0,∴kDB=kDP,
∴点P(4,y1)恒在直线BD上,从而P、B、D三点共线,即BP恒过定点($\frac{5}{2}$,0).
点评 本题考查椭圆方程的求法,考查直线是否过定点的判断与求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题①成立,命题②不成立 | B. | 命题①不成立,命题②成立 | ||
| C. | 命题①和命题②都成立 | D. | 命题①和命题②都不成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α⊥平面β,过α内任意一点作交线的垂线,那么此垂线必垂直于β | |
| D. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
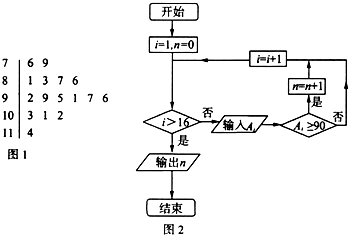 图1是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次是A1,A2,…,A16,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )
图1是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次是A1,A2,…,A16,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )| A. | 6 | B. | 7 | C. | 10 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{{\sqrt{5}}}{2}$x | B. | y=±$\frac{1}{2}$x | C. | y=±$\frac{{\sqrt{5}}}{3}$x | D. | y=±$\frac{{\sqrt{5}}}{4}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com