
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,若直线
时,若直线![]() 是函数
是函数![]() 的图象的切线,求
的图象的切线,求![]() 的最小值;
的最小值;
(2)设函数![]() ,若
,若![]() 在
在![]() 上存在极值,求
上存在极值,求![]() 的取值范围,并判断极值的正负.
的取值范围,并判断极值的正负.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 在
在![]() 上存在极值,且极值都为正数.
上存在极值,且极值都为正数.
【解析】
(1) 设切点坐标为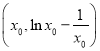 ,求得切线的方程,由直线
,求得切线的方程,由直线![]() 是函数
是函数![]() 的图象的切线,得到
的图象的切线,得到![]() ,
,![]() ,求得
,求得![]() ,利用导数即可求得
,利用导数即可求得![]() 的最小值.
的最小值.
(2)![]() 求出
求出![]() 的导数
的导数![]() ,令
,令![]() ,若
,若![]() 在
在![]() 上存在极值,则
上存在极值,则![]() 或
或 ,分类讨论,分别构造新函数,根据导数与函数的关系,即可求得
,分类讨论,分别构造新函数,根据导数与函数的关系,即可求得![]() 的取值范围.
的取值范围.
(1)设切点坐标为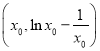 ,
,
![]() ,
,
切线斜率![]() ,又
,又![]() ,
,
![]() ,
,![]()
令![]() ,
,
![]() ,
,
解![]() 得
得![]() ,解
,解![]() 得
得![]() ,
,![]() 在
在![]() 上递减,在
上递减,在![]() 上递增.
上递增.
![]() ,
,![]() 的最小值为
的最小值为![]() .
.
(2)![]() ,
,![]() .
.
![]() .
.
设![]() ,则
,则![]() .
.
由![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
且![]() ,
,![]() ,
,![]() .
.
显然![]() .
.
结合函数图象可知,若![]() 在
在![]() 上存在极值,
上存在极值,
则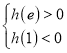 或
或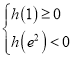
(ⅰ)当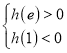 ,即
,即![]() 时,
时,
则必定![]() ,
,![]() ,使得
,使得![]() ,且
,且![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
| - | 0 | + | 0 | - |
| - | 0 | + | 0 | - |
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
∴当![]() 时,
时,![]() 在
在![]() 上的极值为
上的极值为![]() ,
,![]() ,且
,且![]() .
.
![]() .
.
设![]() ,其中
,其中![]() ,
,![]() .
.
![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
![]() ,
,![]() .
.
∴当![]() 时,
时,![]() 在
在![]() 上的极值
上的极值![]() .
.
(ⅱ)当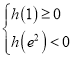 ,即
,即![]() 时,
时,
则必定![]() ,使得
,使得![]() .
.
易知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
此时,![]() 在
在![]() 上的极大值是
上的极大值是![]() ,且
,且![]() .
.
∴当![]() 时,
时,![]() 在
在![]() 上的极值为正数.
上的极值为正数.
综上所述:当![]() 时,
时,![]() 在
在![]() 上存在极值,且极值都为正数.
上存在极值,且极值都为正数.
注:也可由![]() ,得
,得![]() .令
.令![]() 后再研究
后再研究![]() 在
在![]() 上的极值问题.若只求
上的极值问题.若只求![]() 的范围.
的范围.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,若S9=81,a3+a5=14.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,若{bn}的前n项和为Tn,证明:Tn<
,若{bn}的前n项和为Tn,证明:Tn<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 的最大值为
的最大值为![]() ;
;
③![]() 在
在![]() 有
有![]() 个零点;④
个零点;④![]() 在区间
在区间![]() 单调递增.
单调递增.
其中所有正确结论的编号是( )
A.①②B.①③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系xOy中,曲线C的参数方程为![]() (a为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
(a为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.
(1)求C的普通方程和l的倾斜角;
(2)设点![]() ,l和C交于A,B两点,求
,l和C交于A,B两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按![]() /次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第 | 第 | 第 | 第 |
|
收费比率 |
|
|
|
|
|
该公司注册的会员中没有消费超过![]() 次的,从注册的会员中,随机抽取了100位进行统计,得到统计数据如下:
次的,从注册的会员中,随机抽取了100位进行统计,得到统计数据如下:
消费次数 |
|
|
|
|
|
人数 |
|
|
|
|
|
假设汽车美容一次,公司成本为![]() 元,根据所给数据,解答下列问题:
元,根据所给数据,解答下列问题:
(1)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(2)以事件发生的频率作为相应事件发生的概率,设该公司为一位会员服务的平均利润为![]() 元,求
元,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为梯形,AB//CD,
中,底面ABCD为梯形,AB//CD,![]() ,AB=AD=2CD=2,△ADP为等边三角形.
,AB=AD=2CD=2,△ADP为等边三角形.
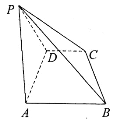
(1)当PB长为多少时,平面![]() 平面ABCD?并说明理由;
平面ABCD?并说明理由;
(2)若二面角![]() 大小为150°,求直线AB与平面PBC所成角的正弦值.
大小为150°,求直线AB与平面PBC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com