练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．已知四棱锥S-ABDC各侧面是全等的等腰三角形且腰长为5cm，顶角45°，求沿棱锥的侧面从A到D的最短路线的长度．

    分析 用空间思维将此正四棱锥的侧面展开，得到一个由3个全等的顶角为45°的等腰三角形组成的图形，所求的路径，是一个以5cm为腰长，135°为顶角的三角形的底边，由余弦定理可得最短路程．

    解答 解：用空间思维将此正四棱锥的侧面展开，得到一个由3个全等的顶角为45°的等腰三角形组成的图形，
    所求的路径，是一个以5cm为腰长，135°为顶角的三角形的底边，
    由余弦定理可得最短路程等于$\sqrt{25+25-2×5×5×cos135°}$=$\sqrt{50-25\sqrt{2}}$cm．

    点评 本题考查正四棱锥的侧面展开图，考查余弦定理，考查学生的计算能力，正确运用正四棱锥的侧面展开图是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．在数列{an}（n=1，2，3，…）中，a1=4，且3，an，an+1成等差数列；
    （1）设bn=an-3，证明：数列{bn}是等比数列；
    （2）设cn=log2（2an-6），记数列{$\frac{1}{{c}_{2n-1}{c}_{2n+1}}$}的前n项和为Tn，证明：Tn$＜\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

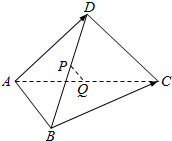    11．如图，P，Q分别为四边形ABCD的对角线BD，AC的中点，$\overrightarrow{BC}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，向量$\overrightarrow{a}$，$\overrightarrow{b}$不共线，试用$\overrightarrow{a}$，$\overrightarrow{b}$表示向量$\overrightarrow{PQ}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．数列{an}满足：a0=8，an=$\frac{1}{2}$an-12，求{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．A，B，C，D，E五人并排站成-排，如果AB之间有且只有2人的排法有36种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．将下列各角由角度转换成弧度．：
    （1）105°；
    （2）-495°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．计算：
    （1）2${\;}^{-\frac{1}{2}}$+$\frac{（-4）^{0}}{\sqrt{2}}$+$\frac{1}{\sqrt{2}-1}$-$\sqrt{（1-\sqrt{5}）^{0}}$；
    （2）log225•log3${\;}^{\frac{1}{16}}$•log5${\;}^{\frac{1}{9}}$；
    （3）（log23+log49+log827+…+log${\;}_{{2}^{n}}$3n）×log9$\root{n}{32}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．如图所示，两根杆分别绕着点A和B（AB=2a）在平面内转动，并且转动时两杆保持互相垂直，求杆的交点P的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知数列{an}满足a1=4．an=4-$\frac{4}{{a}_{n-1}}$（n＞1，n∈N+）记bn=$\frac{1}{{a}_{n}-2}$．
    （1）试判{bn}是否为等差数列？说明理由．
    （2）若an=$\frac{{a}_{n-1}}{4{a}_{n-1}+1}$（n＞1，n∈N+），能否判断数列{$\frac{1}{{a}_{n}}$}是等差数列？

    查看答案和解析>>

    同步练习册答案