
分析 (1)计算b${\;}_{{\;}_{n}}$-bn-1观察结果是否为常数作出判断;
(2)计算$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$观察结果是否为常数作出判断.
解答 解:(1)∵an=4-$\frac{4}{{a}_{n-1}}$,∴an-2=2-$\frac{4}{{a}_{n-1}}$=$\frac{2({a}_{n-1}-2)}{{a}_{n-1}}$,∴$\frac{1}{{a}_{n}-2}$=$\frac{{a}_{n-1}}{2({a}_{n-1}-2)}$.
∴b${\;}_{{\;}_{n}}$-bn-1=$\frac{1}{{a}_{n}-2}$-$\frac{1}{{a}_{n-1}-2}$=$\frac{{a}_{n-1}}{2({a}_{n-1}-2)}$-$\frac{1}{{a}_{n-1}-2}$=$\frac{{a}_{n-1}-2}{2({a}_{n-1}-2)}$=$\frac{1}{2}$.
∴{bn}是等差数列.
(2)∵an=$\frac{{a}_{n-1}}{4{a}_{n-1}+1}$,∴$\frac{1}{{a}_{n}}$=$\frac{4{a}_{n-1}+1}{{a}_{n-1}}$,∴$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=$\frac{4{a}_{n-1}+1}{{a}_{n-1}}$-$\frac{1}{{a}_{n-1}}$=4.
∴{$\frac{1}{{a}_{n}}$}是等差数列.
点评 本题考查了等差数列的判定,数列的递推公式,属于基础题.


科目:高中数学 来源: 题型:解答题
 如图,设四棱柱ABCD-A1B1C1D1的底面为菱形,A1C与底面垂直.过点C作平面与四棱柱的侧棱垂直,且分别交A1A于点E,交BB1于点F,交DD1于点G.
如图,设四棱柱ABCD-A1B1C1D1的底面为菱形,A1C与底面垂直.过点C作平面与四棱柱的侧棱垂直,且分别交A1A于点E,交BB1于点F,交DD1于点G.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
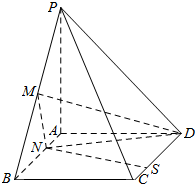 已知四棱锥P-ABCD中,面ABCD为矩形,PA⊥面ABCD,$PA=AD=\frac{1}{2}AB$,M为PB的中点,N、S分别为AB、CD上的点,且$AN=CS=\frac{1}{4}AB$.
已知四棱锥P-ABCD中,面ABCD为矩形,PA⊥面ABCD,$PA=AD=\frac{1}{2}AB$,M为PB的中点,N、S分别为AB、CD上的点,且$AN=CS=\frac{1}{4}AB$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 7月15日 | 8月15日 | 9月15日 | 10月15日 | 11月15日 | 12月15日 |
| 摄氏温度x(℃) | 36 | 35 | 30 | 24 | 18 | 8 |
| 饮料杯数y | 27 | 29 | 24 | 18 | 15 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com