
| ���� | 7��15�� | 8��15�� | 9��15�� | 10��15�� | 11��15�� | 12��15�� |
| �����¶�x���棩 | 36 | 35 | 30 | 24 | 18 | 8 |
| ���ϱ���y | 27 | 29 | 24 | 18 | 15 | 5 |
���� ��1��������һ���ŵ���ͣ����鷢���������¼��Ǵ�6��������ѡȡ2�����ݹ���C62������������������¼��dz鵽���������µ����ݵ������5�֣����ݹŵ���͵ĸ��ʹ�ʽ�õ������
��2���������������ݣ����x��y��ƽ���������������Իع鷽��ϵ���ķ��������ϵ��b����b��x��y��ƽ������������a�Ĺ�ʽ������a��ֵ��д�����Իع鷽�̣�
��3��������������Իع鷽�̣�Ԥ�����Ա���Ϊ35��8ʱ��y��ֵ����Ԥ����ֵͬԭ������������35��8��Ӧ��ֵ�����ľ���ֵ������3���õ����Իع鷽�����룮
��� �⣺��1����鵽���������µ�����Ϊ�¼�A��
�ߴ�6��������ѡȡ2�����ݹ���C62=15�������ÿ������ǵȿ��ܳ��ֵģ����г鵽���������µ����ݵ������5�֣�
��P��A��=$\frac{5}{15}$=$\frac{1}{3}$��
��2�����������$\overline{x}$=27��$\overline{y}$=21���ɹ�ʽ���b=0.7��
��a=21-0.7��27=2.1����y����x�����Իع鷽��Ϊy=0.7x+2.1��
��3����x=35ʱ��y=0.7��35+2.1=26.6��|29-26.6|��3��
��x=8ʱ��y=0.7��8+2.1=7.7��|7.7-5|��3��
���Եõ������Իع鷽���������
���� ���⿼�����Իع鷽�̵�������ȿ����¼��ĸ��ʣ��������Է�����Ӧ�ã�������ʵ���������������һ���ۺ���Ŀ��������Ŀ������Ϊ���������ڸ߿����У�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{8\sqrt{2}}{3}$ | B�� | $\frac{16\sqrt{2}}{3}$ | C�� | $\frac{16}{3}$ | D�� | $\frac{32}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
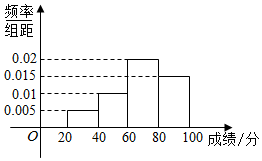 ij��ȫ��ѧ���μ�һ�β��ԣ������÷������η��飺[20��40����[40��60����[60��80����[80��100�������Ƴ���ͼ��ʾ�ijɼ�Ƶ�ʷֲ�ֱ��ͼ��������60�ֵ�������18����ð��ѧ�������ǣ�������
ij��ȫ��ѧ���μ�һ�β��ԣ������÷������η��飺[20��40����[40��60����[60��80����[80��100�������Ƴ���ͼ��ʾ�ijɼ�Ƶ�ʷֲ�ֱ��ͼ��������60�ֵ�������18����ð��ѧ�������ǣ�������| A�� | 50 | B�� | 54 | C�� | 60 | D�� | 64 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{7}$ | B�� | $\frac{4}{7}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{4}{15}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �װ� | �Ұ� | �ϼ� | |
| ���� | |||
| ������ | |||
| �ϼ� |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com