练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
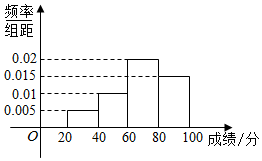
    5．某班全体学生参加一次测试，将所得分数依次分组：[20，40），[40，60），[60，80），[80，100），绘制出如图所示的成绩频率分布直方图，若低于60分的人数是18，则该班的学生人数是（　　）
    A．50B．54C．60D．64

    分析 根据频率分布直方图，求出得分低于60分的频率，再求该班的学生人数．

    解答 解：由频率分布直方图知，得分低于60分的频率为
    （0.005+0.01）×20=0.3，
    ∵低于60分的人数是18，
    ∴该班的学生人数是$\frac{18}{0.3}$=60
    故选：C．

    点评 本题考查了频率分布直方图的应用问题，解题时应根据频率分布直方图求出频率，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    15．（1）“a+c=2b”是“a，b，c成等比数列”的既不充分也不必要条件；
    （2）“$\frac{a}{b}$+$\frac{c}{b}$=2”是“a，b，c成等差数列”的充分不必要条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知直线x-ay=4在y轴上的截距是2，则a等于（　　）
    A．-$\frac{1}{2}$B．$\frac{1}{2}$C．-2D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．在△ABC中，已知三条边上的高线长分别为$\frac{1}{3}$，$\frac{1}{5}$，$\frac{1}{7}$，则△ABC的最大内角为（　　）
    A．$\frac{π}{2}$B．$\frac{2π}{3}$C．$\frac{3π}{4}$D．$\frac{5π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．有一名同学家开了小卖部，他为了研究气温对某种饮料销售的影响，记录了2015年7月至12月每月15号的下午14时的气温和当天卖出的饮料杯数，得到如下资料：
    日期7月15日8月15日9月15日10月15日11月15日12月15日
    摄氏温度x（℃）36353024188
    饮料杯数y27292418155
    改同学确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选中的2组数据进行检验．
    （1）求选取2组数据恰好是相邻两个月的概率；
    （2）若选中的是8月与12月的两组数据，根据剩下的4组数据，求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
    （3）若由线性回归方程得到的估计数据与所选出的检验数据误差不超过3杯，则认为得到的线性回归方程是理想的，请问（2）所得到的线性回归方程是否理想．
    附：对于一组数据（x1，y1），（x2，y2），…，（xn，yn），其回归直线y=bx+a的斜率和截距的最小二乘估计分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}）（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知集合A={x|3≤3x≤27}，B={x|log2x＞1}．
    （1）求（∁RB）∪A；
    （2）已知集合C={x|1＜x＜a}，若 C⊆A，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．sin347°cos148°+sin77°cos58°=（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{3}}{2}$D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．下列命题中真命题的是（　　）
    A．若|a|≠|b|，则a≠-bB．y=cos2x的最小正周期为2π
    C．若M∩N=M，那么M⊆ND．在△ABC中，若$\overrightarrow{AB}$•$\overrightarrow{BC}$＞0，则B为锐角

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．当x=（　　）时，复数z=（x2+x-2）+（x2+3x+2）i（x∈R）是纯虚数．
    A．1B．1或-2C．-1D．-2

    查看答案和解析>>

    同步练习册答案