
分析 (1)解指数不等式我们可以求出集合A,解对数不等式,我们可以求集合B,再由集合补集的运算规则,求出CRB,进而由并集的运算法则,即可求出(CRB)∪A;
(2)由(1)中集合A,结合集合C={x|1<x<a},我们分C=∅和C≠∅两种情况,分别求出对应的实数a的取值,最后综合讨论结果,即可得到答案.
解答 解:(1)A={x|3≤3x≤27}={x|1≤x≤3}…(1分)
B={x|log2x>1}={x|x>2}…(3分)
(CRB)∪A={x|x≤2}∪{x|1≤x≤3}={x|x≤3}…(6分)
(2)当a≤1时,C=∅,此时C⊆A…(8分)
当a>1时,C⊆A,则1<a≤3…(10分)
综上所述,a的取值范围是(-∞,3]…(12分)
点评 本题考查的知识点是集合交、并、补集的混合运算,集合关系中的参数取值问题,指数不等式的解法,对数不等式的解法,其中解指数不等式和对数不等式求出集合A,B是解答本题的关键,在(2)的解答中易忽略C为空集也满足条件而错解为(1,3],也容易忽略最后要的结果为集合,不能用不等式的形式表达.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 3 | C. | -3 | D. | 3或-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{3}{4}$) | B. | (0,$\frac{3}{4}$] | C. | [0,$\frac{3}{4}$] | D. | [0,$\frac{3}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
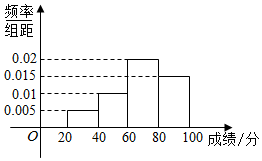 某班全体学生参加一次测试,将所得分数依次分组:[20,40),[40,60),[60,80),[80,100),绘制出如图所示的成绩频率分布直方图,若低于60分的人数是18,则该班的学生人数是( )
某班全体学生参加一次测试,将所得分数依次分组:[20,40),[40,60),[60,80),[80,100),绘制出如图所示的成绩频率分布直方图,若低于60分的人数是18,则该班的学生人数是( )| A. | 50 | B. | 54 | C. | 60 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (1,3) | D. | ($\frac{1}{2}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恰有1个红球与恰有2个红球 | B. | 至少有1个黑球与都是黑球 | ||
| C. | 至少有1个黑球与至少有1个红球 | D. | 至多有1个黑球与都是红球 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com