
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
分析 由题意设三条高对应的三角形边长分别为:a,b,c,则由三角形面积公式可得:$\frac{1}{2}×\frac{1}{3}×$a=$\frac{1}{2}×\frac{1}{5}×$b=$\frac{1}{2}×\frac{1}{7}×c$,化简可得:35a=21b=15c,得b=$\frac{35a}{21}$,c=$\frac{35a}{15}$,C为三角形最大内角,利用余弦定理可求cosC=-$\frac{1}{2}$,结合范围C∈(0,π),即可解得C的值.
解答 解:∵在△ABC中,已知三条边上的高线长分别为$\frac{1}{3}$,$\frac{1}{5}$,$\frac{1}{7}$,
∴设三条高对应的三角形边长分别为:a,b,c,则由三角形面积公式可得:$\frac{1}{2}×\frac{1}{3}×$a=$\frac{1}{2}×\frac{1}{5}×$b=$\frac{1}{2}×\frac{1}{7}×c$,化简可得:35a=21b=15c,
∴解得:b=$\frac{35a}{21}$,c=$\frac{35a}{15}$,C为三角形最大内角,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{{a}^{2}+(\frac{35a}{21})^{2}-(\frac{35a}{15})^{2}}{2×a×\frac{35a}{21}}$=-$\frac{1}{2}$,
∵C∈(0,π),
∴C=$\frac{2π}{3}$.
故选:B.
点评 本题主要考查了三角形面积公式,余弦定理,特殊角的三角函数值在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{3}{4}$) | B. | (0,$\frac{3}{4}$] | C. | [0,$\frac{3}{4}$] | D. | [0,$\frac{3}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
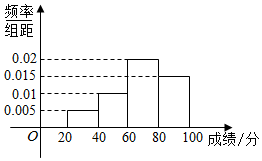 某班全体学生参加一次测试,将所得分数依次分组:[20,40),[40,60),[60,80),[80,100),绘制出如图所示的成绩频率分布直方图,若低于60分的人数是18,则该班的学生人数是( )
某班全体学生参加一次测试,将所得分数依次分组:[20,40),[40,60),[60,80),[80,100),绘制出如图所示的成绩频率分布直方图,若低于60分的人数是18,则该班的学生人数是( )| A. | 50 | B. | 54 | C. | 60 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{1}{8}$ | C. | -$\frac{1}{8}$ | D. | 以上都不正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com