
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①根据根式的运算法则和性质进行判断,
②根据根式的运算法则进行判断,
③根据指数幂的运算法则进行求解.
解答 解::①$\root{n}{a^n}=a$;当n为正奇数时(n≥2),等式成立,当n为正偶函数,$\root{n}{{a}^{n}}$=|a|,此时不成立,故①错误,
②由条件得a≥0,则$\sqrt{a\root{3}{a}}=\sqrt{a•{a}^{\frac{1}{3}}}$=$\sqrt{{a}^{\frac{4}{3}}}$═${a}^{\frac{2}{3}}$,故$\sqrt{a\root{3}{a}}={a^{\frac{2}{3}}}$正确;
③若x3=4,则x=$\root{3}{4}$,故③错误,
故选:B.
点评 本题主要考查命题的真假判断,涉及根式和指数幂的运算,根据相应的运算法则是解决本题的关键.比较基础.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
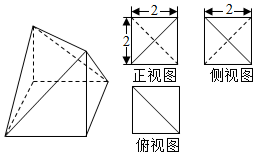 已知某几何体的直观图及三视图如图所示,三视图的轮廓均为正方形,则该几何体的表面积为( )
已知某几何体的直观图及三视图如图所示,三视图的轮廓均为正方形,则该几何体的表面积为( )| A. | 14+2$\sqrt{3}$ | B. | 12+4$\sqrt{3}$ | C. | 16+4$\sqrt{3}$ | D. | 15+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x+$\frac{4}{x}$ | B. | y=sinx+$\frac{4}{sinx}$(0<x<π) | ||
| C. | y=ex+4e-x | D. | y=$\sqrt{{x}^{2}+3}$+$\frac{2}{\sqrt{{x}^{2}+3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3] | B. | [-1,8] | C. | (0,6] | D. | [2,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com