
| A. | 33% | B. | 49% | C. | 62% | D. | 88% |
分析 利用等差数列的通项公式与求和公式即可得出.
解答 解:由题意可得:每日的织布量形成等差数列{an},且a1=5,a30=1,
设公差为d,则1=5+29d,解得d=-$\frac{4}{29}$.
∴S10=5×10+$\frac{10×9}{2}×(-\frac{4}{29})$=$\frac{1270}{29}$.
S30=$\frac{30×(5+1)}{2}$=90.
∴该女子到第10日时,大约已经完成三十日织布总量的$\frac{1270}{29}$×$\frac{1}{90}$≈0.49=49%.
故选:B.
点评 本题考查了等差数列的通项公式及其求和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
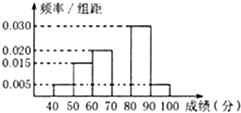 某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如图频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]).
某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如图频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a⊥b,α∥β,则b⊥β | B. | 若b?β,a⊥b,则α⊥β | C. | 若a⊥b,α⊥β,则b∥β | D. | 若b⊥β,α∥β,则a⊥b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com