
分析 (Ⅰ)通过讨论a的符号,求出a的值即可;
(Ⅱ)令h(x)=f(2x+1)-f(x-1),通过讨论x的范围,得到函数的单调性,求出h(x)的最小值,从而求出m的范围即可.
解答 解:(Ⅰ)显然a≠0,…(1分)
当a>0时,解集为$[-\frac{1}{a},\frac{3}{a}]$,$-\frac{1}{a}=-6,\frac{3}{a}=2$,无解;…(3分)
当a<0时,解集为$[\frac{3}{a},-\frac{1}{a}]$,
令$-\frac{1}{a}=2,\frac{3}{a}=-6$,$a=-\frac{1}{2}$,
综上所述,$a=-\frac{1}{2}$.…(5分)
(Ⅱ) 当a=2时,
令h(x)=f(2x+1)-f(x-1)
=|4x+1|-|2x-3|
=$\left\{\begin{array}{l}{-2x-4,x≤-\frac{1}{4}}\\{6x-2,-\frac{1}{4}<x<\frac{3}{2}}\\{2x+4,x≥\frac{3}{2}}\end{array}\right.$
…(7分)
由此可知,h(x)在$(-∞,-\frac{1}{4})$单调减,在$(-\frac{1}{4},\frac{3}{2})$单调增,在$(\frac{3}{2},+∞)$单调增,
则当$x=-\frac{1}{4}$时,h(x)取到最小值 $-\frac{7}{2}$,…(8分)
由题意知,$-\frac{7}{2}≤7-3m$,则实数m的取值范围是$({-∞,\frac{7}{2}}]$…(10分)
点评 本题考查了解绝对值不等式问题,考查分段函数以及分类讨论思想,是一道中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | aiaj≤akal | B. | aiaj≥akal | C. | SiSj<SkSl | D. | SiSj≥SkSl |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 人员编号 | 1 | 2 | 3 | 4 | 5 |
| (x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,1,1) | (1,2,1) |
| 人员编号 | 6 | 7 | 8 | 9 | 10 |
| (x,y,z) | (1,2,2) | (1,1,1) | (1,2,2) | (1,0,0) | (1,1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{ab+bc+ac}{{a}^{2}+{b}^{2}+{c}^{2}}$ | B. | -$\frac{ab+bc+ac}{{a}^{2}+{b}^{2}+{c}^{2}}$ | ||
| C. | $\frac{2ab}{{a}^{2}+{b}^{2}}$ | D. | -$\frac{2ab}{{a}^{2}+{b}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
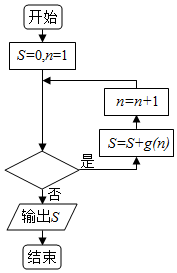 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.在如图所示的程序框图中,若输出的结果S=$\frac{2016}{2017}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.在如图所示的程序框图中,若输出的结果S=$\frac{2016}{2017}$,则判断框中可以填入的关于n的判断条件是( )| A. | n≤2016? | B. | n≤2017? | C. | n>2016? | D. | n>2017? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com