Question

4．空间四边形ABCD中，AB=CD=2，且异面直线AB和CD成30°角，E，F分别为BC，AD中点，则EF的长为$\frac{\sqrt{6}±\sqrt{2}}{2}$．

Answer 1

分析 画出空间四边形ABCD，并连接BD，取BD中点G，连接EG，FG，根据已知条件及异面直线所成角的概念知道：∠EGF=30°，或150°，EG=FG=1，所以根据余弦定理即可求出EF．

解答 解：如图，连接BD，取BD中点G，连接FG，EG，则：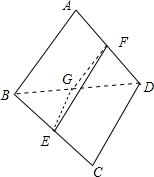
GF∥AB，EG∥CD，GF=EG=1；
∴∠EGF或其补角便是异面直线AB，CD所成角；
∠EGF=30°，或150°；
∴在△EFG中，由余弦定理可得：$E{F}^{2}=1+1±2•\frac{\sqrt{3}}{2}$=2$±\sqrt{3}$=$\frac{3±2\sqrt{3}+1}{2}=（\frac{\sqrt{3}±1}{\sqrt{2}}）^{2}$；
∴$EF=\frac{\sqrt{3}±1}{\sqrt{2}}=\frac{\sqrt{6}±\sqrt{2}}{2}$．
故答案为：$\frac{\sqrt{6}±\sqrt{2}}{2}$．

点评 考查中位线的性质，异面直线所成角的概念，异面直线所成角的范围，以及余弦定理，并且对于$2±\sqrt{3}$，能写成$（\frac{\sqrt{3}±1}{\sqrt{2}}）^{2}$的形式．