
 942+…+0.94n–1)
942+…+0.94n–1) .
.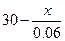 ≥0,即x≤1.8时,bn+1≤bn≤…≤b1=30
≥0,即x≤1.8时,bn+1≤bn≤…≤b1=30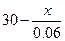 <0,即x>1.8时,
<0,即x>1.8时,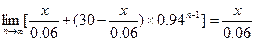
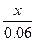 .
. 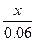 ≤60,所以x≤3.6
≤60,所以x≤3.6

 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源:不详 题型:解答题
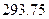 m?
m?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
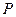 从原点出发,沿
从原点出发,沿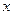 轴正向移动距离
轴正向移动距离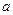 到达
到达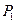 ,再沿
,再沿 轴正向移动距离
轴正向移动距离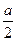 点,到达
点,到达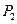 点,再沿
点,再沿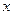 轴正向移动
轴正向移动 到达
到达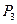 点,
点,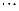 依次类推无限进行每转1次距离缩小一半.
依次类推无限进行每转1次距离缩小一半.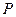 行进路线的极限;
行进路线的极限;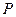 与坐标平面上哪1点无限接近?
与坐标平面上哪1点无限接近?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
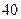 %,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
%,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化. 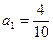 ,经过
,经过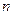 年后绿化的面积为
年后绿化的面积为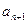 ,试用
,试用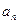 表示
表示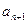 ;
;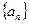 的第
的第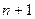 项
项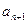 ;
;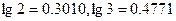 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com