
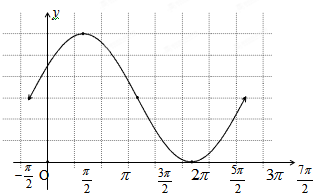
分析 (1)$\frac{x}{2}$+$\frac{π}{6}$=0,$\frac{π}{2}$,π,$\frac{3π}{2}$,2π得到相应的x的值,列表描点即可;
(2)由函数y=Asin(ωx+φ)+b变换规律,将y=3sin$\frac{x}{2}$沿x轴向左平移$\frac{π}{3}$单位可得:y=3sin$\frac{1}{2}$(x+$\frac{π}{3}$)=3sin($\frac{x}{2}$+$\frac{π}{6}$),将y=3sin$\frac{1}{2}$(x+$\frac{π}{3}$)沿y轴向上平移3个单位可得:f(x)=3sin($\frac{x}{2}$+$\frac{π}{6}$)+3的图象,根据图象写出周期,由 2kπ-$\frac{π}{2}$≤$\frac{x}{2}$+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,求得x的范围,即得单调增区间,
(3)由x∈[$\frac{π}{3}$,$\frac{4π}{3}$],$\frac{x}{2}$+$\frac{π}{6}$∈[$\frac{π}{3}$,$\frac{5π}{6}$],根据正弦函数的图象及性质可知:3sin($\frac{x}{2}$+$\frac{π}{6}$)+3∈[$\frac{9}{2}$,6].
解答 解:(1)令$\frac{x}{2}$+$\frac{π}{6}$=0,$\frac{π}{2}$,π,$\frac{3π}{2}$,2π,得到相应的x的值,列表如下:
| x | -$\frac{π}{3}$ | $\frac{2π}{3}$ | $\frac{5π}{3}$ | $\frac{8π}{3}$ | $\frac{11π}{3}$ |
| $\frac{x}{2}$+$\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| y | 3 | 6 | 3 | 0 | 3 |
 …6分
…6分点评 本题考查用五点法作y=Asin(ωx+φ)+b的图象,以及函数的性质、图象变换,用五点法作y=Asin(ωx+φ)+b的图象,是解题的关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 9 | C. | 13 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平行四边形ABCD中,E和F分别是边CD和BC的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
在平行四边形ABCD中,E和F分别是边CD和BC的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>2} | B. | {x|0<x<2} | C. | {x|x>$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 第1行 | 1 |
| 第2行 | 2 4 8 |
| 第3行 | 16 32 64 128 256 |
| … | … |
| A. | 229 | B. | 230 | C. | 231 | D. | 232 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com