
| A. | 5 | B. | 9 | C. | 13 | D. | 16 |
分析 根据等比数列的性质得到Sn,S2n-Sn,S3n-S2n成等比,列出关系式,又S6:S3=3,表示出S3,代入到列出的关系式中即可求出S9:S6的值.
解答 解:因为等比数列{an}的前n项和为Sn,
则Sn,S2n-Sn,S3n-S2n成等比,(Sn≠0)
所以$\frac{{S}_{6}-{S}_{3}}{{S}_{3}}$=$\frac{{S}_{9}-{S}_{6}}{{S}_{6}-{S}_{3}}$,又 $\frac{S_6}{S_3}=4$,即S3=$\frac{1}{4}$S6,
所以$\frac{{S}_{6}-\frac{1}{4}{S}_{6}}{\frac{1}{4}{S}_{6}}$=$\frac{{S}_{9}-{S}_{6}}{{S}_{6}-\frac{1}{4}{S}_{6}}$,
整理得S9=$\frac{13}{4}$S6,
∴$\frac{S_9}{S_3}$=$\frac{\frac{13}{4}}{\frac{1}{4}}$=13.
故选:C.
点评 此题考查学生灵活运用等比数列的性质化简求值,是一道基础题.解本题的关键是根据等比数列的性质得到Sn,S2n-Sn,S3n-S2n成等比.


科目:高中数学 来源: 题型:选择题
 在一次某地区中学联合考试后,汇总了3217名文科考生的数学成绩,用a1,a2,…,a3217表示,我们将不低于120的考分叫“优分”,将这些数据按图的程序框图进行信息处理,则输出的数据为这3217名考生的( )
在一次某地区中学联合考试后,汇总了3217名文科考生的数学成绩,用a1,a2,…,a3217表示,我们将不低于120的考分叫“优分”,将这些数据按图的程序框图进行信息处理,则输出的数据为这3217名考生的( )| A. | 平均分 | B. | “优分”人数 | ||
| C. | “优分”率 | D. | “优分”人数与非“优分”人数的比值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 1 | C. | $\frac{5}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
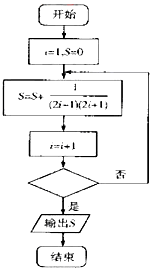
| A. | i>2014 | B. | i>2014 | C. | i>2015 | D. | i>2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com