
| A. | {x|x>2} | B. | {x|0<x<2} | C. | {x|x>$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$} |
分析 根据两个不等式的关系,只要令$\frac{1}{t}$=x,则关于t的不等式ln$\frac{1}{t}$>$\frac{a}{t}$-1,得到$\frac{1}{t}$的范围,即求得x的范围.
解答 解:令$\frac{1}{t}$=x,则关于t的不等式ln$\frac{1}{t}$>$\frac{a}{t}$-1
即lnt<1-$\frac{a}{t}$的解集为{$\frac{1}{t}$|$\frac{1}{t}$>2},
所以所以{t|0<t<$\frac{1}{2}$},
所以不等式lnx<1-$\frac{a}{x}$的解集为{x|0<x<$\frac{1}{2}$};
故选D.
点评 本题考查了抽象不等式的解法;本题的关键是发现两个不等式的未知数关系是倒数关系.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:选择题
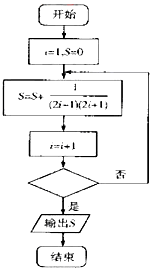
| A. | i>2014 | B. | i>2014 | C. | i>2015 | D. | i>2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
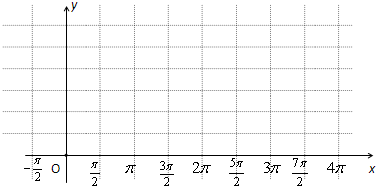
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com