
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
分析 由题意对函数的变化规律进行探究,发现呈周期性的变化,且其周期是4,故只须研究清楚f2010(x)是一个周期中的第几个函数即可得出其解析式.
解答 解:由题意f0(x)=sinx,f1(x)=f0′(x)=cosx,f2(x)=f1′(x)=-sinx,f3(x)=f2′(x)=-cosx,f4(x)=f3′(x)=sinx,由此可知,在逐次求导的过程中,所得的函数呈周期性变化,从0开始计,周期是4,∵2017=4×504+1,f2010(x)是一周中的第三个函数,故f2017(x)=cosx.
故选:C.
点评 本题考查函数的周期性,探究过程中用的是归纳推理,对其前几项进行研究得出规律,求解本题的关键一是要归纳推理的意识,一是对正、余弦函数的导数求法公式熟练掌握.本题易因为判断不准f2017(x)一周期中的第几个数而导致错误,要谨慎.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
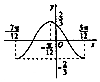 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{12}$)=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{12}$)=( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com