
【题目】已知a≥3,函数F(x)=min{2|x﹣1|,x2﹣2ax+4a﹣2},其中min(p,q)= ![]()
(1)求使得等式F(x)=x2﹣2ax+4a﹣2成立的x的取值范围
(2)(1)求F(x)的最小值m(a)
(3)求F(x)在[0,6]上的最大值M(a)
【答案】
(1)
由a≥3,故x≤1时,
x2﹣2ax+4a﹣2﹣2|x﹣1|=x2+2(a﹣1)(2﹣x)>0;
当x>1时,x2﹣2ax+4a﹣2﹣2|x﹣1|=x2﹣(2+2a)x+4a=(x﹣2)(x﹣2a),
则等式F(x)=x2﹣2ax+4a﹣2成立的x的取值范围是(2,2a)
(2)
(1)设f(x)=2|x﹣1|,g(x)=x2﹣2ax+4a﹣2,
则f(x)min=f(1)=0,g(x)min=g(a)=﹣a2+4a﹣2.
由﹣a2+4a﹣2=0,解得a=2+ ![]() (负的舍去),
(负的舍去),
由F(x)的定义可得m(a)=min{f(1),g(a)},
即m(a)= ![]()
(3)
当0≤x≤2时,F(x)≤f(x)≤max{f(0),f(2)}=2=F(2);
当2<x≤6时,F(x)≤g(x)≤max{g(2),g(6)}
=max{2,34﹣8a}=max{F(2),F(6)}.
则M(a)= ![]()
【解析】(1)由a≥3,讨论x≤1时,x>1,去掉绝对值,化简x2﹣2ax+4a﹣2﹣2|x﹣1|,判断符号,即可得到F(x)=x2﹣2ax+4a﹣2成立的x的取值范围;(2)(1)设f(x)=2|x﹣1|,g(x)=x2﹣2ax+4a﹣2,求得f(x)和g(x)的最小值,再由新定义,可得F(x)的最小值;(2)分别对当0≤x≤2时,当2<x≤6时,讨论F(x)的最大值,即可得到F(x)在[0,6]上的最大值M(a).本题考查新定义的理解和运用,考查分类讨论的思想方法,以及二次函数的最值的求法,不等式的性质,考查化简整理的运算能力,属于中档题.
【考点精析】根据题目的已知条件,利用函数的最值及其几何意义的相关知识可以得到问题的答案,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.


科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且![]() .将角α的终边按逆时针方向旋转
.将角α的终边按逆时针方向旋转![]() ,交单位圆于点B.记A(x1,y1),B(x2,y2).
,交单位圆于点B.记A(x1,y1),B(x2,y2).
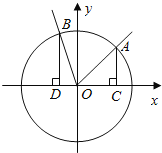
(Ⅰ)若![]() ,求x2;
,求x2;
(Ⅱ)分别过A,B作x轴的垂线,垂足依次为C,D.记△AOC的面积为S1,△BOD的面积为S2.若S1=2S2,求角α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=xa的图象过点(2,4).
(1)求函数f(x)的解析式;
(2)设函数h(x)=4f(x)-kx-8在[5,8]上是单调函数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列满足|an﹣ ![]() |≤1,n∈N* .
|≤1,n∈N* .
(1)求证:|an|≥2n﹣1(|a1|﹣2)(n∈N*)
(2)若|an|≤( ![]() )n , n∈N* , 证明:|an|≤2,n∈N* .
)n , n∈N* , 证明:|an|≤2,n∈N* .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
(1)请将上表数据补充完整;函数![]() 的解析式为
的解析式为![]() (直接写出结果即可);
(直接写出结果即可);
(2)根据表格中的数据作出![]() 一个周期的图象;
一个周期的图象;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设锐角三角形的内角A,B,C的对边分别为a、b、c,且sinA-cosC=cos(A-B).
(1)求B的大小;
(2)求cosA+sinC的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2+bx+c(a≠0),满足条件f(x+1)-f(x)=2x(x∈R),且f(0)=1.
(Ⅰ)求f(x)的解析式;
(Ⅱ)当x≥0时,f(x)≥mx-3恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com