

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数个 |
分析 把正子体分成两个四棱锥,分别求两个四棱锥的体积,根据底面的范围,得到正子体的体积在一个取值范围中,不是一个定值,即可得出结论.
解答 解:设ABCD与正方体的截面四边形为A′B′C′D′,
设AA′=x(0≤x≤1),则AB′=1-x,|AD|2=x2+(1-x)2=2(x-$\frac{1}{2}$)2+$\frac{1}{2}$
故SABCD=|AD|2∈[$\frac{1}{2}$,1]
V=$\frac{1}{3}$SABCD•h•2=$\frac{1}{3}$SABCD∈[$\frac{1}{6}$,$\frac{1}{3}$].
∴该八面体的体积可能值有无数个,
故选:D.
点评 本题主要考查求棱锥的体积,体现了转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | [2,+∞) | C. | [0,+∞) | D. | (-∞,-2]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
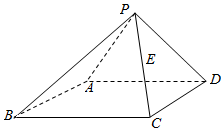 如图所示,在四棱锥P-ABCD中,ABCD为矩形,PA⊥PD,平面PAD⊥平面ABCD,且AB=6,AD=4,PA=PD,E位PC的中点
如图所示,在四棱锥P-ABCD中,ABCD为矩形,PA⊥PD,平面PAD⊥平面ABCD,且AB=6,AD=4,PA=PD,E位PC的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥2 | B. | a≥-2 | C. | a≥0 | D. | a<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com