
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
分析 设需要n天时间才能打穿$\frac{{2}^{n}-1}{2-1}$+$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$≥1000,化为:2n-$\frac{2}{{2}^{n}}$-999≥0,令f(n)=2n-$\frac{2}{{2}^{n}}$-999,利用函数零点存在定理与函数的单调性即可得出
解答 解:设需要n天时间才能打穿,则$\frac{{2}^{n}-1}{2-1}$+$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$≥1000,
化为:2n-$\frac{2}{{2}^{n}}$-999≥0,
令f(n)=2n-$\frac{2}{{2}^{n}}$-999,则f(10)=1024-$\frac{1}{512}$-999>0.
f(9)=512-$\frac{1}{256}$-999<0.
f(x)=${2}^{x}-\frac{2}{{2}^{x}}$-999,(x≥1).
∴f(x)在(9,10)内存在一个零点.
又函数f(x)在x≥1时单调递增,因此f(x)在(9,10)内存在唯一一个零点.
∴需要10天时间才能打穿.
故选:C.
点评 本题考查了函数零点存在定理与函数的单调性、等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:选择题
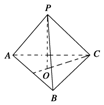 已知点P是正三角形ABC所在平面外一点,PA=PB=PC=$\frac{2}{3}$,AB=1,则PC和平面ABC所成的角是( )
已知点P是正三角形ABC所在平面外一点,PA=PB=PC=$\frac{2}{3}$,AB=1,则PC和平面ABC所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $5\sqrt{2}$ | D. | $7\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{8}$ | B. | $\frac{25}{4}$ | C. | 25 | D. | $\frac{4}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向右平行移动$\frac{π}{3}$个单位长 | ||
| C. | 向左平行移动$\frac{π}{9}$个单位长度 | D. | 向右平行移动$\frac{π}{9}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=$\overrightarrow{0}$ | |
| B. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|且$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$=$\overrightarrow{b}$ | |
| C. | 若|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,则$\overrightarrow{a}$⊥$\overrightarrow{b}$ | |
| D. | 若向量$\overrightarrow{b}$与向量$\overrightarrow{a}$共线,则有且只有一个实数λ,使得$\overrightarrow{b}$=λ$\overrightarrow{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com