
【题目】已知边长为![]() 的正方形
的正方形![]() 与菱形
与菱形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() 为
为![]() 中点.
中点.
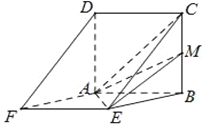
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,求四面体
,求四面体![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)∵四边形![]() 是正方形,证得
是正方形,证得![]() ∥平面
∥平面![]() ,
, ![]() ∥平面
∥平面![]() ,即可利用面面平行的判定定理,证得
,即可利用面面平行的判定定理,证得![]() 平面
平面![]() ,进而得到
,进而得到![]() 平面
平面![]() ;
;
(2)取![]() 中点
中点![]() ,连结
,连结![]() ,证的
,证的![]() 平面
平面![]() ,得到
,得到![]() 为四面体
为四面体![]() 的高,然后利用等体积法求解即可.
的高,然后利用等体积法求解即可.
试题解析:
(1)∵四边形ABCD是正方形,∴BC∥AD.∵BC![]() 平面ADF,AD平面ADF,
平面ADF,AD平面ADF,
∴BC∥平面ADF.∵四边形ABEF是菱形,
∴BE∥AF.
∵BE![]() 平面ADF,AF平面ADF,
平面ADF,AF平面ADF,
∴BE∥平面ADF.∵BC∥平面ADF,BE∥平面ADF,BC∩BE=B,
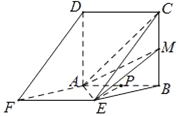
∴平面BCE∥平面ADF.
∵EM平面BCE,∴EM∥平面ADF.
(2)取AB中点P,连结PE.∵在菱形ABEF中,∠ABE=60°,
∴△AEB为正三角形,∴EP⊥AB.∵AB=2,∴EP=![]() .
.
∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,
∴EP⊥平面ABCD, ∴EP为四面体E﹣ACM的高.
∴![]()
![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为  为参数),以坐标原点为极点, x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
为参数),以坐标原点为极点, x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为 ![]() .直线l过点
.直线l过点 ![]() .
.
(1)若直线l与曲线C交于A,B两点,求 ![]() 的值;
的值;
(2)求曲线C的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n分别是先后抛掷一枚骰子所得到的点数,则在先后两次出现的点数中有5的情况下,方程x2+mx+n=0有实根的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某高传染性病毒流行期间,为了建立指标来显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数x≤3;②标准差s≤2;③平均数x≤3且标准差s≤2;④平均数x≤3且极差小于或等于2;⑤众数等于1且极差小于或等于4.
A. ①② B. ③④ C. ③④⑤ D. ④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来发展的新机遇.2016年618期间,某购物平台的销售业绩高达516亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(Ⅰ)先完成关于商品和服务评价的2×2列联表,再判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
(Ⅱ)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为随机变量X:
①求对商品和服务全好评的次数X的分布列;
②求X的数学期望和方差.
附临界值表:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
K2的观测值:k= ![]() (其中n=a+b+c+d)
(其中n=a+b+c+d)
关于商品和服务评价的2×2列联表:
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | a=80 |
|
|
对商品不满意 |
| d=10 |
|
合计 |
|
| n=200 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示的圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形的圆心角均为![]() ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.

乙商场:从装有2个白球、2个蓝球和2个红球(这些球除颜色外完全相同)的盒子中一次性摸出2球,若摸到的是2个相同颜色的球,则为中奖.
试问:购买该商品的顾客在哪家商场中奖的可能性大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地上年度电价为0.8元,年用电量为1亿千瓦时.本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至x元,则本年度新增用电量y(亿千瓦时)与(x﹣0.4)元成反比例.又当x=0.65时,y=0.8.
(1)求y与x之间的函数关系式;
(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益=用电量×(实际电价﹣成本价)].
查看答案和解析>>
科目:高中数学 来源: 题型:
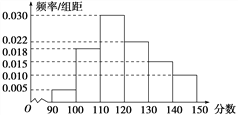
【题目】某校100名学生的数学测试成绩的频率分布直方图如图所示,分数不低于a即为优秀,如果优秀的人数为20,则a的估计值是( )
A. 130 B. 140 C. 133 D. 137
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在山顶![]() 点已测得
点已测得![]() ,
,![]() ,
,![]() 的俯角分别为
的俯角分别为![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() 为山脚两侧共线的三点,现欲沿直线
为山脚两侧共线的三点,现欲沿直线![]() 开通穿山隧道,为了求出隧道
开通穿山隧道,为了求出隧道![]() 的长,至少还需要直接测量出
的长,至少还需要直接测量出![]() ,
,![]() ,
,![]() 中的哪些线段长?把你上一问指出的需要测量得线段长和已测得的角度作为已知量,写出计算隧道
中的哪些线段长?把你上一问指出的需要测量得线段长和已测得的角度作为已知量,写出计算隧道![]() 的步骤.
的步骤.

解:
步骤![]() :还需要直接测量得线段为.
:还需要直接测量得线段为.
步骤![]() :计算线段.
:计算线段.
计算步骤:
步骤![]() :计算线段
:计算线段
计算步骤:
步骤![]() :计算线段
:计算线段
计算步骤:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com