
【题目】已知直线l的参数方程为  为参数),以坐标原点为极点, x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
为参数),以坐标原点为极点, x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为 ![]() .直线l过点
.直线l过点 ![]() .
.
(1)若直线l与曲线C交于A,B两点,求 ![]() 的值;
的值;
(2)求曲线C的内接矩形的周长的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】中国科学院亚热带农业生态研究所2017年10月16日正式发布一种水稻新种质,株高可达2.2米以上,具有高产、抗倒伏、抗病虫害、酎淹涝等特点,被认为开启了水稻研制的一扇新门.以下是![]() 两组实验田中分别抽取的6株巨型稻的株高,数据如下(单位:米).
两组实验田中分别抽取的6株巨型稻的株高,数据如下(单位:米).
![]() : 1.7 1.8 1.9 2.2 2.4 2.5
: 1.7 1.8 1.9 2.2 2.4 2.5
![]() : 1.8 1.9 2.0 2.0 2.4 2.5
: 1.8 1.9 2.0 2.0 2.4 2.5
(1)绘制![]() 两组数据的茎叶图,并求出
两组数据的茎叶图,并求出![]() 组数据的中位数和
组数据的中位数和![]() 组数据的方差;
组数据的方差;
(2)从![]() 组样本中随机抽取2株,请列出所有的基本事件,并求至少有一株超过
组样本中随机抽取2株,请列出所有的基本事件,并求至少有一株超过![]() 组株高平均值的概率.
组株高平均值的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),直线
为参数),直线 ![]() 的方程为
的方程为 ![]() ,以
,以 ![]() 为极点,以
为极点,以 ![]() 轴正半轴为极轴,建立极坐标系,
轴正半轴为极轴,建立极坐标系,
(1)求曲线 ![]() 和直线
和直线 ![]() 的极坐标方程;
的极坐标方程;
(2)若直线 ![]() 与曲线
与曲线 ![]() 交于
交于 ![]() 两点,求
两点,求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=![]() ,AB=
,AB=![]() ,AC=2,A1C1=1,
,AC=2,A1C1=1,![]() .
.
(1)证明:BC![]() A1D;
A1D;
(2)求二面角A-CC1-B的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
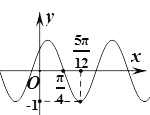
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,为了得到
)的部分图象如图所示,为了得到![]() 的图象,只要将
的图象,只要将![]() 的图象
的图象
A. 先向右平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
B. 先向右平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
C. 先向左平移![]() 个单位长度 ,再把所得各点的横坐标缩短到原来的
个单位长度 ,再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
D. 先向左平移![]() 个单位长度, 再把所得各点的横坐标缩短到原来的
个单位长度, 再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(Ⅰ)试问:一共有多少种不同的结果?请列出所有可能的结果;
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com