
°æƒø°øΩ¸ƒÍ¿¥Œ“π˙µÁ◊”…ÌҖ–“µ”≠¿¥∑¢’𵃖¬ª˙”ˆ£Æ2016ƒÍ618∆⁄º‰£¨ƒ≥π∫ŒÔ∆Ωœ˙ €“µº®∏þ¥Ô516“⁄»À√Ò±“£Æ”Î¥ÀÕ¨ ±£¨œýπÿπпÌ≤ø√≈Õ∆≥ˆ¡À’Î∂‘µÁ…õƒ…Ã∆∑∫Õ∑˛ŒÒµƒ∆¿º€ÃÂœµ£Æœ÷¥”∆¿º€œµÕ≥÷–—°≥ˆ200¥Œ≥…π¶Ωª“◊£¨≤¢∂‘∆‰∆¿º€Ω¯––Õ≥º∆£¨∂‘…Ã∆∑µƒ∫√∆¿¬ Œ™0.6£¨∂‘∑˛ŒÒµƒ∫√∆¿¬ Œ™0.75£¨∆‰÷–∂‘…Ã∆∑∫Õ∑˛ŒÒ∂º◊ˆ≥ˆ∫√∆¿µƒΩª“◊Œ™80¥Œ£Æ
£®¢Ò£©œ»ÕÍ≥…πÿ”⁄…Ã∆∑∫Õ∑˛ŒÒ∆¿º€µƒ2°¡2¡–¡™±Ì£¨‘Ÿ≈–∂œƒÐ∑Ò‘⁄∑∏¥ÌŒÛµƒ∏≈¬ ≤ª≥¨π˝0.001µƒ«∞÷œ¬£¨»œŒ™…Ã∆∑∫√∆¿”Î∑˛ŒÒ∫√∆¿”–πÿ£ø
£®¢Ú£©»ÙΩ´∆µ¬ ”Œ™∏≈¬ £¨ƒ≥»À‘⁄∏√π∫ŒÔ∆Ωî…œΩ¯––µƒ3¥Œπ∫ŒÔ÷–£¨…Ë∂‘…Ã∆∑∫Õ∑˛ŒÒ»´∫√∆¿µƒ¥Œ ˝Œ™Àʪ˙±‰¡øX£∫
¢Ÿ«Û∂‘…Ã∆∑∫Õ∑˛ŒÒ»´∫√∆¿µƒ¥Œ ˝Xµƒ∑÷≤º¡–£ª
¢⁄«ÛXµƒ ˝—ß∆⁄Õ˚∫Õ∑Ω≤Ó£Æ
∏Ω¡ŸΩÁ÷µ±Ì£∫
P£®K2°ðk£© | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
K2µƒπ€≤‚÷µ£∫k= ![]() £®∆‰÷–n=a+b+c+d£©
£®∆‰÷–n=a+b+c+d£©
πÿ”⁄…Ã∆∑∫Õ∑˛ŒÒ∆¿º€µƒ2°¡2¡–¡™±Ì£∫
∂‘∑˛ŒÒ∫√∆¿ | ∂‘∑˛ŒÒ≤ª¬˙“‚ | ∫œº∆ | |
∂‘…Ã∆∑∫√∆¿ | a=80 |
|
|
∂‘…Ã∆∑≤ª¬˙“‚ |
| d=10 |
|
∫œº∆ |
|
| n=200 |
°æ¥∞∏°øΩ‚£∫£®¢Ò£©”…“‚ø…µ√πÿ”⁄…Ã∆∑∫Õ∑˛ŒÒ∆¿º€µƒ2°¡2¡–¡™±Ì»Áœ¬£∫
∂‘∑˛ŒÒ∫√∆¿ | ∂‘∑˛ŒÒ≤ª¬˙“‚ | ∫œº∆ | |
∂‘…Ã∆∑∫√∆¿ | 80 | 40 | 120 |
∂‘…Ã∆∑≤ª¬˙“‚ | 70 | 10 | 80 |
∫œº∆ | 150 | 50 | 200 |
K2= ![]() °÷11.111£æ10.828
°÷11.111£æ10.828
π ƒÐ‘⁄∑∏¥ÌŒÛµƒ∏≈¬ ≤ª≥¨π˝0.001µƒ«∞÷œ¬£¨»œŒ™…Ã∆∑∫√∆¿”Î∑˛ŒÒ∫√∆¿”–πÿ£Æ
£®¢Ú£©¢Ÿ√ø¥Œπ∫ŒÔ ±£¨∂‘…Ã∆∑∫Õ∑˛ŒÒ∂º∫√∆¿µƒ∏≈¬ Œ™0.4£¨«“Xµƒ»°÷µø…“‘ «0£¨1£¨2£¨3£Æ
∆‰÷–P£®X=0£©=0.63= ![]() £ª P£®X=1£©=C310.40.62=
£ª P£®X=1£©=C310.40.62= ![]() £ª
£ª
P£®X=2£©=C320.420.6= ![]() £ª P£®X=3£©=C330.43=
£ª P£®X=3£©=C330.43= ![]() £Æ
£Æ
Xµƒ∑÷≤º¡–Œ™£∫
X | 0 | 1 | 2 | 3 |
P | | | | |
¢⁄”…”⁄X°´B£®3£¨0.4£©£¨‘ÚE£®X£©=3°¡0.4=1.2£¨D£®X£©=3°¡0.4°¡0.6=0.72
°æΩ‚Œˆ°ø£®¢Ò£©”…“—÷™¡–≥ˆπÿ”⁄…Ã∆∑∫Õ∑˛ŒÒ∆¿º€µƒ2°¡2¡–¡™±Ì£¨¥˙»Îπ´ Ω«Ûµ√k2µƒ÷µ£¨∂‘”¶ ˝±Ìµ√¥∞∏£ª£®¢Ú£©¢Ÿ√ø¥Œπ∫ŒÔ ±£¨∂‘…Ã∆∑∫Õ∑˛ŒÒ»´∫√∆¿µƒ∏≈¬ Œ™0.4£¨«“Xµƒ»°÷µø…“‘ «0£¨1£¨2£¨3£¨X°´B£®3£¨0.4£©£Æ«Û≥ˆœý”¶µƒ∏≈¬ £¨ø…µ√∂‘…Ã∆∑∫Õ∑˛ŒÒ»´∫√∆¿µƒ¥Œ ˝Xµƒ∑÷≤º¡–£®∏≈¬ ”√◊È∫œ ˝À„ Ω±Ì æ£©£ª¢⁄¿˚”√∂˛œÓ∑÷≤ºµƒ ˝—ß∆⁄Õ˚∫Õ∑Ω≤Ó«ÛXµƒ ˝—ß∆⁄Õ˚∫Õ∑Ω≤Ó£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝ ![]() .
.
£®¢Ò£©»Ù∫Ø ˝ ![]() ”–º´÷µ£¨«Û µ ˝
”–º´÷µ£¨«Û µ ˝ ![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®¢Ú£©µ± ![]() ”–¡Ω∏ˆº´÷µµ„£®º«Œ™
”–¡Ω∏ˆº´÷µµ„£®º«Œ™ ![]() ∫Õ
∫Õ ![]() £© ±£¨«Û÷§£∫
£© ±£¨«Û÷§£∫ ![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=|x+2|+|x|
£®1£©Ω‚≤ªµ» Ωf£®x£©°Ð4£ª
£®2£©»Ù∂‘x° R£¨∫„”–f£®x£©£æ|3a©Å1|≥…¡¢£¨«Ûaµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡À∂‘ƒ≥øŒÃ‚Ω¯––Ã÷¬€—–æø£¨”√∑÷≤„≥È—˘µƒ∑Ω∑®¥”»˝À˘∏þ–£A°¢B°¢Cµƒœýπÿ»À‘±÷–£¨≥È»°»Ù∏…»À◊È≥…—–æø–°◊È£¨”–πÿ ˝æðº˚œ¬±Ì(µ•Œª£∫»À)
∏þ–£ | œýπÿ»À ˝ | ≥È»°»À ˝ |
A | x | 1 |
B | 36 | y |
C | 54 | 3 |
(1)«Ûx°¢y£ª
(2)»Ù¥”∏þ–£Bœýπÿµƒ»À÷–—°2»À◊˜◊®Ã‚∑¢—‘£¨”¶≤…”√ ≤√¥≥È—˘∑®£¨«Î–¥≥ˆ∫œ¿Ìµƒ≥È—˘π˝≥ãÆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®±æ¬˙∑÷12∑÷£©º◊°¢““¡ΩŒª—ß…˙≤Œº” ˝—ßæ∫»¸≈ý—µ£¨œ÷∑÷±¥”À˚√«‘⁄≈ý—µ∆⁄º‰≤Œº”µƒ»Ù∏…¥Œ‘§»¸≥…º®÷–Àʪ˙≥È»°8¥Œ£¨º«¬º»Áœ¬£∫
º◊ 82 81 79 78 95 88 93 84
““ 92 95 80 75 83 80 90 85
£®1£©”√æ•“∂Õº±Ì æ’‚¡Ω◊È ˝æð£ª
£®2£©œ÷“™¥”÷–—°≈…“ª»À≤Œº” ˝—ßæ∫»¸£¨¥”Õ≥º∆—ßµƒΩ«∂»£®‘⁄∆Ωæ˘ ˝°¢∑Ω≤ÓªÚ±Í◊º≤Ó÷–—°¡Ω∏ˆ£©∑÷Œˆ£¨ƒ„»œŒ™—°≈…ƒƒŒª—ß…˙≤Œº”∫œ £ø«ÎÀµ√˜¿Ì”…
≤Œøºπ´ Ω£∫![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™±þ≥§Œ™![]() µƒ’˝∑Ω–Œ
µƒ’˝∑Ω–Œ![]() ”Ρ‚–Œ
”Ρ‚–Œ![]() À˘‘⁄∆Ω√ʪ•œý¥π÷±£¨
À˘‘⁄∆Ω√ʪ•œý¥π÷±£¨ ![]() Œ™
Œ™![]() ÷–µ„£Æ
÷–µ„£Æ
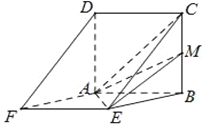
£®1£©«Û÷§£∫ ![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®2£©»Ù![]() ,«ÛÀƒ√ÊÃÂ
,«ÛÀƒ√ÊÃÂ![]() µƒÃª˝£Æ
µƒÃª˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬¡–Àƒ∏ˆΩ·¬€£∫ ¢Ÿ»Ùx£æ0£¨‘Úx£æsinx∫„≥…¡¢£ª
¢⁄°∞»Ùam2£ºbm2 £¨ ‘Úa£ºb°±µƒƒÊ√¸Ã‚Œ™’Ê√¸Ã‚
¢€m° R£¨ πf£®x£©=£®m©Å1£©x ![]() «√ð∫Ø ˝£¨«“‘⁄£®©Å°Þ£¨0£©…œµ•µ˜µðºı
«√ð∫Ø ˝£¨«“‘⁄£®©Å°Þ£¨0£©…œµ•µ˜µðºı
¢Ð∂‘”⁄√¸Ã‚p£∫x° R πµ√x2+x+1£º0£¨‘Ú©Vp£∫x° R£¨æ˘”–x2+x+1£æ0
∆‰÷–’˝»∑Ω·¬€µƒ∏ˆ ˝ «£® £©
A.1∏ˆ
B.2∏ˆ
C.3∏ˆ
D.4∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄º´◊¯±Íœµœ¬£¨“—÷™«˙œþC1£∫¶—=cos¶»+sin¶»∫Õ«˙œþC2£∫¶—sin£®¶»©Å ![]() £©=
£©= ![]() £Æ
£Æ
£®1£©«Û«˙œþC1∫Õ«˙œþC2µƒ÷±Ω«◊¯±Í∑Ω≥ãª
£®2£©µ±¶»° £®0£¨¶–£© ±£¨«Û«˙œþC1∫Õ«˙œþC2π´π≤µ„µƒ“ª∏ˆº´◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©= ![]() ax2©Ålnx©Å2£Æ
ax2©Ålnx©Å2£Æ
£®1£©µ±a=1 ±£¨«Û«˙œþf£®x£©‘⁄µ„£®1£¨f£®1£©£©¥¶µƒ«–œþ∑Ω≥ãª
£®2£©»Ùa£æ0£¨«Û∫Ø ˝f£®x£©µƒµ•µ˜«¯º‰£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com