【题目】双曲线 
﹣ 
=1（a＞0，b＞0）的左、右焦点分别为F1 ， F2 ， P为双曲线上一点，且 
=0，△F1PF2的内切圆半径r=2a，则双曲线的离心率e= ．
【答案】5
【解析】解：可设P为第一象限的点，
由双曲线的定义可得|PF1|﹣|PF2|=2a，①
=0，可得PF1⊥PF2 ，
由勾股定理可得|PF1|2+|PF2|2=|F1F2|2=4c2 ， ②
②﹣①2 ， 可得2|PF1||PF2|=4c2﹣4a2=4b2 ，
即有|PF1|+|PF2|= 
，
由三角形的面积公式可得 
r（|PF1|+|PF2|+|F1F2|）= |PF1||PF2|，
即为2a（ +2c）=2b2 ，
即有c+2a= 
，两边平方可得
c2+4a2+4ac=c2+b2=c2+c2﹣a2 ，
即c2﹣4ac﹣5a2=0，解得c=5a（c=﹣a舍去），
即有e= 
=5．
所以答案是：5．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】某班同学利用寒假进行社会实践活动，对
岁的人群随机抽取
人进行了一次生活习惯是
否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得
到如下统计表和各年龄段人数频率分布直方图：
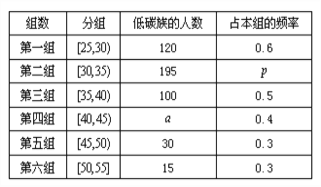
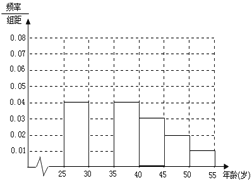
（I）补全频率分布直方图并求、
、
的值；
（II）从年龄段在
的“低碳族”中采用分层抽样法抽取
人参加户外低碳体验活动，其中选取
人作为领队，求选取的名领队中恰有1人年龄在
岁的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，
为正方体，给出以下五个结论：
① 
平面
；
② 
⊥平面；
③ 与底面
所成角的正切值是
；
④ 二面角
的正切值是；
⑤ 过点
且与异面直线
和 
均成70°角的直线有4条．
其中，所有正确结论的序号为________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．已知曲线C的参数方程为： 
（φ为参数），直线l的极坐标方程为ρ（cosθ+sinθ）=4．
（1）求曲线C的普通方程和直线l的直角坐标方程；
（2）若点P在曲线C上，点Q在直线l上，求线段PQ的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
： 
与抛物线
交于
， 
两点，记抛物线在
， 
两点处的切线
， 
的交点为
．
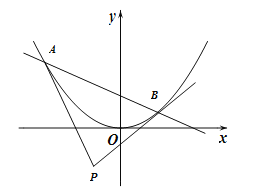
（I）求证: 
；
（II）求点
的坐标(用
， 
表示)；
（Ⅲ）若
，求△
的面积的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在（0，+∞）上的函数f（x）=a（x+ 
）﹣|x﹣ |（a∈R）．
（1）当a= 
时，求f（x）的单调区间；
（2）若f（x）≥ x对任意的x＞0恒成立，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知平面内圆心为
的圆的方程为
，点
是圆上的动点，点
是平面内任意一点，若线段
的垂直平分线交直线
于点
，则点
的轨迹可能是_________．（请将下列符合条件的序号都填入横线上）
①椭圆；②双曲线；③抛物线；④圆；⑤直线；⑥一个点.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若a和b是计算机在区间（0，2）上产生的均匀随机数，则一元二次不等式ax2+4x+4b＞0（a＞0）的解集不是R的概率为（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com