
已知抛物线 y2=2x,直线l过点(0,2)与抛物线交于M,N两点,以线段MN的长为直径的圆过坐标原点O,求直线l的方程.
y2=2x,直线l过点(0,2)与抛物线交于M,N两点,以线段MN的长为直径的圆过坐标原点O,求直线l的方程.
科目:高中数学 来源: 题型:
若双曲线的渐近线方程为y=±3x,它的一个焦点是(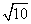 ,0),则双曲线的方程是_ ___________.
,0),则双曲线的方程是_ ___________.
椭圆的两个焦点为F1、F2,短轴的一个端点为A,且三角形F1AF2是顶角为120°的等腰三角形,则此椭圆的离心率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
双曲线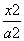 -
-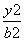 =1 (a>0,b>0)的左、右焦点分别是F1,F2,过F1作倾斜角为30°的直 线交双曲线右支于M点,若MF2垂直于x轴,则双曲线的离心率为________.
=1 (a>0,b>0)的左、右焦点分别是F1,F2,过F1作倾斜角为30°的直 线交双曲线右支于M点,若MF2垂直于x轴,则双曲线的离心率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
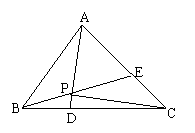 如图,在正ΔABC中,点D、E分别在边BC, AC上,且
如图,在正ΔABC中,点D、E分别在边BC, AC上,且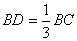 ,
,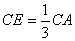 ,AD,BE相交于点P.
,AD,BE相交于点P.
求证:(I) 四点P、D、C、E共 圆;
(II) AP ⊥CP。
查看答案和解析>>
科目:高中数学 来源: 题型:
 某班级从甲乙两位同学选派一人参加数学竞赛,老师对他们平时的10次模拟测试成绩(单位:分)进行了记录如下:
某班级从甲乙两位同学选派一人参加数学竞赛,老师对他们平时的10次模拟测试成绩(单位:分)进行了记录如下:
甲:79 83 96 89 86 78 85 95 82 87
乙:81 95 83 76 91 86 96 77 82 93
(1)用茎叶图表示这两组数据,并分别求出这两组数据
的中位数;
(2)分别计算这两组数据的平均数和方差,并根据你的计
算结果,判断选派哪位学生参加合适?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com