
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
分析 先求出$\overrightarrow{a}$+$\overrightarrow{b}$的坐标,设$\overrightarrow{c}$=(x,y,z),根据题中的条件求出x+2y+3z=-7,即$\overrightarrow{a}$•$\overrightarrow{c}$=-7,再利用两个向量的夹角公式,设$\overrightarrow{a}$、$\overrightarrow{c}$ 的夹角等于θ,求出cosθ的值,由此求得θ的值.
解答 解:∵向量$\overrightarrow{a}$=(1,2,3),$\overrightarrow{b}$=(-2,-4,-6),|
∴$\overrightarrow{a}$+$\overrightarrow{b}$=(-1,-2,-3).
设$\overrightarrow{c}$=(x,y,z),
由($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$=7,可得 (-1,-2,-3)•(x,y,z)=-x-2y-3y=7,
∴x+2y+3z=-7,即$\overrightarrow{a}$•$\overrightarrow{c}$=-7,
设$\overrightarrow{a}$、$\overrightarrow{c}$ 的夹角等于θ,则cosθ=$\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{a}|•|\overrightarrow{c}|}$=$\frac{-7}{\sqrt{1+4+9}•\sqrt{14}}$=-$\frac{1}{2}$.
再由0°≤θ≤180°,可得θ=120°.
故选:C.
点评 本题主要考查两个向量的夹角公式的应用,求出$\overrightarrow{a}$•$\overrightarrow{c}$=-7是解题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{13}}}{2}$ | C. | $\frac{{\sqrt{15}}}{2}$ | D. | $\frac{{\sqrt{19}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (-∞,2) | C. | (3,+∞) | D. | (-∞,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
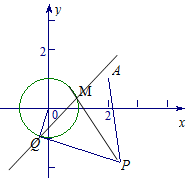 已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,PM,切点为Q,M,且满足|PQ|=|PA|.
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,PM,切点为Q,M,且满足|PQ|=|PA|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com