
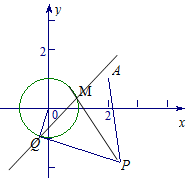
 已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,PM,切点为Q,M,且满足|PQ|=|PA|.
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,PM,切点为Q,M,且满足|PQ|=|PA|.分析 (1)由已知Q为切点,可知PQ⊥OQ,结合勾股定理有|PQ|2=|OP|2-|OQ|2及已知|PQ|=|PA|,利用两点间的距离公式可得a,b之间的关系
(2)设圆P的半径为R,由圆P与圆O有公共点,且半径最小,可知R=OP,利用两点间的距离,结合(1)中a,b的关系可转化为关于a的二次形式,结合二次函数的性质可求R的最小值,进而可求圆的方程;
(3)求出直线MQ的方程,结合b=3-2a,即可得出结论.
解答 解:(1)连OP,∵Q为切点,PQ⊥OQ,由勾股定理有|PQ|2=|OP|2-|OQ|2.
∵|PQ|=|PA|故PA2=PO2-1
∴a2+b2-1=(a-2)2+(b-1)2
化简可得,2a+b-3=0
(2)设圆P的半径为R,
∵圆P与圆O有公共点,且半径最小,
∴R=|OP|=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{a}^{2}+(-2a+3)^{3}}$=$\sqrt{5(a-\frac{6}{5})^{2}+\frac{9}{5}}$,
故当a=$\frac{6}{5}$时,|OP|min=$\frac{3\sqrt{5}}{5}$
此时,b=$\frac{3}{5}$,Rmin=$\frac{3\sqrt{5}}{5}$-1.
得半径取最小值时圆P的方程为$(x-\frac{6}{5})^{2}+(y-\frac{3}{5})^{2}=(\frac{3\sqrt{5}}{5}-1)^{2}$;
(3)设Q(x1,y1),M(x2,y2),则
$\left\{\begin{array}{l}{{{x}_{1}}^{2}+{{y}_{1}}^{2}=1}\\{\frac{b-{y}_{1}}{a-{x}_{1}}•\frac{{y}_{1}}{{x}_{1}}=-1}\end{array}\right.$化简得ax1+by1=1,
同理ax2+by2=1.
所以,直线MQ的方程为ax+by=1.
∵b=3-2a,代入上式得(x-2y)a+3y-1=0,
令x-2y=0,3y-1=0,得x=$\frac{2}{3}$,y=$\frac{1}{3}$,
∴直线MQ过定点($\frac{2}{3},\frac{1}{3}$).
点评 本题主要考查了圆的性质的简单应用,还考查了一定的逻辑推理与运算的能力,试题具有一定的综合性.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,7) | B. | (9,25) | C. | (13,49) | D. | (9,49) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ | B. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{6}$ | C. | x=$\frac{1}{3}$,y=$\frac{1}{6}$,z=$\frac{1}{3}$ | D. | x=$\frac{1}{6}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com