
分析 (1)设t=log3x,得到t∈[-1,1],从而求出f(x)的解析式和函数的定义域即可;
(2)设u=3x,得到$u∈[\frac{1}{3},3]$,求出f(u),从而求出函数的值域即可;
(3)求出a2-3a+3∈[3,7],从而求出a的范围即可.
解答 解:(1)设t=log3x,t∈[-1,1],则x=3t-------(3分)
f(t)=(3t)2-2•3t+4,
∴f(x)=(3x)2-2•3x+4,
f(x)的定义域为[-1,1]---(6分)
(2)设u=3x,$u∈[\frac{1}{3},3]$,
f(u)=u2-2u+4=(u-1)2+3,
∴f(u)∈[3,7]
即所求值域为[3,7]----------(9分)
(3)由于方程f(x)=a2-3a+3有实数根,
∴a2-3a+3∈[3,7],
∴a∈[-1,0]∪[3,4]-----------(12分)
点评 本题考查了对数函数以及指数函数的性质,考查函数的定义域、值域问题,是一道中档题.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=1,g(x)=x0 | B. | f(x)=x-1,g(x)=$\frac{x^2}{x}$-1 | ||
| C. | f (x)=x2,g(x)=($\sqrt{x}$)4 | D. | f(x)=|x|,g(x)=$\sqrt{x^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,7) | B. | (9,25) | C. | (13,49) | D. | (9,49) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | [0,+∞) | C. | (-∞,0] | D. | (-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
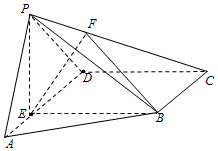 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [1,+∞) | C. | (-∞,0]∪(1,+∞) | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com