
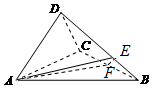
 在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC上,且BD=3BE,BC=2BF.
在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC上,且BD=3BE,BC=2BF.分析 (1)由已知求解直角三角形可得AC⊥BC.再由平面ACD⊥平面ABC,结合面面垂直的性质得BC⊥平面ACD,从而得AD⊥BC;
(2)取线段AC的中点O,连接DO,由AD=CD,得DO⊥AC.再由平面ACD⊥平面ABC,可得DO⊥平面ABC,然后求出三棱锥D-ABC和A-EBF的体积,利用等积法作差求得VA-EFCD,则答案可求.
解答 (1)证明:在Rt△ADC中,AD=DC=2,AD⊥DC,∴$AC=2\sqrt{2}$,
在△ABC中,∵∠BAC=45°,AB=4,
∴BC2=AC2+AB2+2AC•AB•cos45°=${(2\sqrt{2})^2}+{4^2}-2×2\sqrt{2}×4×\frac{{\sqrt{2}}}{2}=8$,
可得:$AC=BC=2\sqrt{2}$,∴AC2+BC2=AB2.则AC⊥BC.
又∵平面ACD⊥平面ABC,平面ACD∩平面ABC=AC,
∴BC⊥平面ACD,得AD⊥BC;
(2)解:取线段AC的中点O,连接DO,
∵AD=CD,∴DO⊥AC.
又∵平面ACD⊥平面ABC,
平面ACD∩平面ABC=AC,DO?平面ACD,∴DO⊥平面ABC,
$DO=\sqrt{2}$,${S_{△ABC}}=\frac{1}{2}AC•BC=\frac{1}{2}×2\sqrt{2}×2\sqrt{2}=4$,
∴VD-ABC=$\frac{1}{3}{S_{△ABC}}•DO$=$\frac{1}{3}×\frac{1}{2}×2\sqrt{2}×2\sqrt{2}$=$\frac{{4\sqrt{2}}}{3}$,
过点E作EG∥DO交BO于G,∴EG⊥平面ABC,
∵BD=3BE,∴$EG=\frac{1}{3}DO=\frac{{\sqrt{2}}}{3}$,
∵BC=2BF,∴$BF=\frac{1}{2}BC=\sqrt{2}$,
VA-EBF═$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×2\sqrt{2}×\frac{{\sqrt{2}}}{3}$=$\frac{{2\sqrt{2}}}{9}$,
∴VA-EFCD=VD-ABC-VE-ABF=$\frac{{10\sqrt{2}}}{9}$,
∴平面AEF将三棱锥D-ABC分成的两部分的体积之比$\frac{{10\sqrt{2}}}{9}:\frac{{2\sqrt{2}}}{9}=5:1$.
点评 本题考查空间中直线与直线的位置关系,考查了线面垂直的判定,训练了利用等积法求多面体的体积,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | ($\frac{1}{7}$,$\frac{2}{7}$) | C. | ($\frac{2}{7}$,$\frac{1}{7}$) | D. | ($\frac{1}{7}$,$\frac{1}{14}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1365石 | B. | 338石 | C. | 168石 | D. | 134石 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
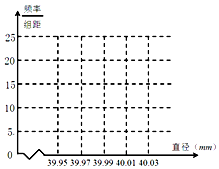 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如表频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如表频率分布表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 6 | P1 |
| [39.97,39.99) | 12 | 0.20 |
| [39.99,40.01) | a | 0.50 |
| [40.01,40.03) | b | P2 |
| 合计 | n | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={x^{\frac{1}{2}}}$ | B. | y=x2 | C. | y=-x|x| | D. | y=x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com