
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
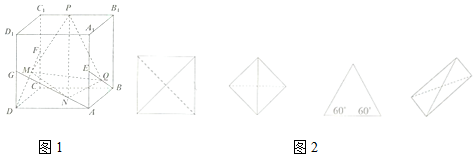
分析 根据已知中点E、F、G分别是正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点,点M、N、Q、P分别在线段DF、AG、BE、C1B1上.结合正投影的画法,分析三棱锥P-MNQ的俯视图形状,可得答案.
解答 解:在底面ABCD上考察,P、M、N、Q四点在俯视图中它们分别在BC、CD、DA、AB上,
先考察形状,再考察俯视图中的实虚线,可判断C不可能,
因为该等腰三角形且当中无虚线,说明有两个顶点投到底面上重合了,
只能是Q、N投射到点A或者M、N投射到点D,
此时俯视图不可能是等腰三角形.
故选:C.
点评 本题考查的知识点是简单空间图形的三视图,其中熟练掌握正投影的画法,是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | $(\frac{9}{4},+∞)$ | B. | $[\frac{9}{4},+∞)$ | C. | $(-∞,\frac{9}{4})$ | D. | $(-∞,\frac{9}{4}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α和β都垂直于同一平面 | |
| B. | α内不共线的三点到β的距离相等 | |
| C. | l,m是平面α内的直线且l∥β,m∥β | |
| D. | l,m是两条异面直线且l∥α,m∥α,m∥β,l∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
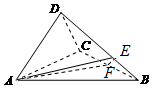 在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC上,且BD=3BE,BC=2BF.
在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC上,且BD=3BE,BC=2BF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 06 | B. | 10 | C. | 25 | D. | 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知正方形ABCD的边长为1,如图所示:
已知正方形ABCD的边长为1,如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com