
分析 (1)令x=2+$\sqrt{2}$cosα,y=$\sqrt{2}$sinα-1,消去参数α,得到点A的轨迹方程,判断A的轨迹;
(2)将直线C的极坐标方程化为普通方程,根据公共点个数判断出直线与圆相切,列出方程解出a.
解答 解:(1)令x=2+$\sqrt{2}$cosα,y=$\sqrt{2}$sinα-1,则cosα=$\frac{x-2}{\sqrt{2}}$,sinα=$\frac{y+1}{\sqrt{2}}$,
∴$\frac{(x-2)^{2}}{2}$+$\frac{(y+1)^{2}}{2}$=1,即(x-2)2+(y+1)2=2.
∴A的轨迹是以(2,-1)为圆心,以$\sqrt{2}$为半径的圆.
(2)∵ρcos(θ-$\frac{π}{4}$)=$\sqrt{2}$a,∴$\frac{\sqrt{2}}{2}ρcosθ$+$\frac{\sqrt{2}}{2}ρsinθ$=$\sqrt{2}a$,即ρcosθ+ρsinθ-2a=0.
∴直线C的普通方程为x+y-2a=0.
∵直线C与动点A的轨迹有且仅有一个公共点,
∴$\frac{|2-1-2a|}{\sqrt{2}}$=$\sqrt{2}$,解得a=-$\frac{1}{2}$或a=$\frac{3}{2}$.
点评 本题考查了极坐标方程,参数方程化普通方程,属于基础题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
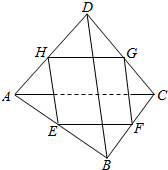 如图所示,在空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,判断平面EG与直线BD是否平行?平面EG与直线AC是否平行?直线BD与直线AC是什么位置关系?
如图所示,在空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,判断平面EG与直线BD是否平行?平面EG与直线AC是否平行?直线BD与直线AC是什么位置关系?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,e) | B. | (0,$\frac{1}{e}$) | C. | (0,$\frac{1}{e}$),($\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$),(e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com