
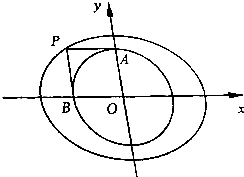
 ��֪��ԲC1��$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{6}$=1��ԲC2��x2+y2=4������ԲC1�ϵ�P��ԲC2���������ߣ��е�ΪA��B��
��֪��ԲC1��$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{6}$=1��ԲC2��x2+y2=4������ԲC1�ϵ�P��ԲC2���������ߣ��е�ΪA��B������ ��1����A��x1��y1����B��x2��y2������PA��PB�ķ��̷ֱ�Ϊx1x+y1y=4��x2x+y2y=4����PA��PB����P��-2��2�����ɴ������AB��ֱ�߷��̣�
��2�����ֱ��AB�ķ���x0x+y0y=4�������x��y��Ľ��㣬�Ӷ��ɵ������ε���������û�������ʽ������ֵ��P�����꣮
��� �⣺��1����A��x1��y1����B��x2��y2����
��OA��PA���ɵ�����PA��y-y1=-$\frac{{x}_{1}}{{y}_{1}}$��x-x1����
x12+y12=4��
����ɵ�x1x+y1y=4��
ͬ��PB�ķ���x2x+y2y=4��
��PA��PB����P��-2��2����
��-2x1+2y1=4��-2x2+2y2=4��
������ȷ��һ��ֱ�ߣ��ɵ�AB��ֱ�߷���Ϊ��-2x+2y=4��
��Ϊx-y+4=0��
��2���ɣ�1���ɵ�ֱ��AB�ķ���Ϊx0x+y0y=4��
��x=0���ɵ�y=$\frac{4}{{y}_{0}}$����y=0���ɵ�x=$\frac{4}{{x}_{0}}$��
�����������S=$\frac{1}{2}$|$\frac{4}{{y}_{0}}$|•|$\frac{4}{{x}_{0}}$|=|$\frac{8}{{x}_{0}{y}_{0}}$|��
��$\frac{1}{3\sqrt{2}}$|x0y0|=2|$\frac{{x}_{0}}{2\sqrt{3}}$•$\frac{{y}_{0}}{\sqrt{6}}$|��$\frac{{{x}_{0}}^{2}}{12}$+$\frac{{{y}_{0}}^{2}}{6}$=1��
����|x0y0|��3$\sqrt{2}$��
��S��$\frac{4\sqrt{2}}{3}$��
���ҽ���|y0|=$\frac{\sqrt{2}}{2}$|x0|ʱ����$\frac{{{x}_{0}}^{2}}{12}$+$\frac{{{y}_{0}}^{2}}{6}$=1��
����P��$\frac{\sqrt{2}}{2}$��$\frac{1}{2}$������-$\frac{\sqrt{2}}{2}$��$\frac{1}{2}$������-$\frac{\sqrt{2}}{2}$��-$\frac{1}{2}$������$\frac{\sqrt{2}}{2}$��$\frac{1}{2}$����
�����ε����Sȡ����СֵΪ$\frac{4\sqrt{2}}{3}$��
���� ���⿼��ֱ�ߺ�Բ��λ�ù�ϵ����Ҫ�����߷��̵������������ε��������ֵ��ע�����û�������ʽ���������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{36}$=1��x��0�� | B�� | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1��x��0�� | ||
| C�� | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{25}$=1��x��0�� | D�� | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1��x��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{��}{8}$ | C�� | $\frac{��}{4}$ | D�� | $\frac{��}{6}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com