
分析 利用等差数列的定义、等比数列的定义、向量的模、向量的夹角及数列的前n项和等知识对每个结论逐一判断可得答案.
解答 解:∵|$\overrightarrow{{a}_{n}}$|=$\sqrt{{x}_{n}^{2}+{y}_{n}^{2}}$,
∴|$\overrightarrow{{a}_{n+1}}$|=$\sqrt{{x}_{n+1}^{2}+{y}_{n+1}^{2}}$=$\sqrt{(\frac{{x}_{n}-{y}_{n}}{2})^{2}+(\frac{{x}_{n}+{y}_{n}^{\;}}{2})^{2}}$=$\frac{\sqrt{2}}{2}$=$\sqrt{{x}_{n}^{2}+{y}_{n}^{2}}$=|$\overrightarrow{{a}_{n}}$|,
∴{|${\overrightarrow{a_n}}$|}是以$\sqrt{2}$为首项,以$\frac{\sqrt{2}}{2}$为公比的等比数列,即①不正确.
又∵{|${\overrightarrow{a_n}}$|}是以$\sqrt{2}$为首项,以$\frac{\sqrt{2}}{2}$为公比的等比数列,
∴②|${\overrightarrow{a_2}}$|•|${\overrightarrow{a_6}}$|=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$×$\sqrt{2}$×($\frac{\sqrt{2}}{2}$)5=$\frac{1}{4}$,即②不正确.
又∵{|${\overrightarrow{a_n}}$|}是以$\sqrt{2}$为首项,以$\frac{\sqrt{2}}{2}$为公比的等比数列,
∴|${\overrightarrow{a_n}}$|=2×($\frac{\sqrt{2}}{2}$)n,
∴$\overrightarrow{{a}_{1}}$=$\sqrt{2}$,$\overrightarrow{{a}_{2}}$=1,n≥3时,${\overrightarrow{a_n}}$<1
∴c1=1,c2=0,当n≥3时,cn<0,
∴当n=1或2时,Tn取得最大值为1,
∴③不正确.
由已知得:$\overrightarrow{{a}_{n-1}}$•$\overrightarrow{{a}_{n}}$=(xn-1,yn-1)•$\frac{1}{2}$(xn-1-yn-1,xn-1+yn-1)=$\frac{1}{2}$(xn-12+yn-12)=$\frac{1}{2}$|$\overrightarrow{{a}_{n-1}}$|2,
又∵cos<$\overrightarrow{{a}_{n-1}}$•$\overrightarrow{{a}_{n}}$>=$\frac{\overrightarrow{{a}_{n-1}}•\overrightarrow{{a}_{n}}}{|\overrightarrow{{a}_{n-1}}||\overrightarrow{{a}_{n}}|}$,
将|$\overrightarrow{{a}_{n}}$|=$\frac{\sqrt{2}}{2}$|$\overrightarrow{{a}_{n-1}}$|,$\overrightarrow{{a}_{n-1}}$•$\overrightarrow{{a}_{n}}$=$\frac{1}{2}$|$\overrightarrow{{a}_{n-1}}$|2,代入可得cos<$\overrightarrow{{a}_{n-1}}$•$\overrightarrow{{a}_{n}}$>=$\frac{\sqrt{2}}{2}$,
向量$\overrightarrow{a_n}$与$\overrightarrow{{a_{n-1}}}$的夹角为θn(n≥2),均有θn=$\frac{π}{4}$.
∴④正确.
故所有正确结论的序号是④,
故答案为:④
点评 本题主要考查知识间的转化与应用,涉及到数列的判断与证明,通项公式及前n项和公式的灵活运用.这是高考考查的重点,在学习中要重点关注.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
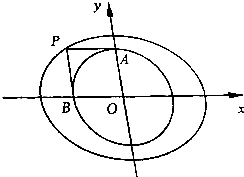 已知椭圆C1:$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{6}$=1,圆C2:x2+y2=4.过椭圆C1上点P作圆C2的两条切线,切点为A,B.
已知椭圆C1:$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{6}$=1,圆C2:x2+y2=4.过椭圆C1上点P作圆C2的两条切线,切点为A,B.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 8 | C. | 12 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f({m}^{n})}{{m}^{n}}$ | B. | logmn•f(lognm) | C. | $\frac{f({n}^{m})}{{n}^{m}}$ | D. | lognm•f(logmn) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com