
分析 (I)对AB有无斜率进行讨论,联立方程组消元,根据x1+x2=2列方程判断有无解;
(II)设AB方程y=kx+b,联立方程组消元,根据x1+x2=2得出k,b的关系,代入弦长公式得出|AB|,求出AB的中点,得出AB的中垂线方程解出M的坐标,根据$\frac{|AB|}{d}$=$\sqrt{3}$列方程解出k,得出AB方程.
解答 解:(I)①若直线AB无斜率,则AB方程为x=1.
联立方程组$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$.
即A(1,2),B(1,-2).
∴|AB|=4.
②若直线AB有斜率,设直线AB的斜率为k,则直线AB的方程为:y=k(x-1),
联立方程组$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,消元得:k2x2-(2k2+4)x+k2=0,
∴x1+x2=$\frac{2{k}^{2}+4}{{k}^{2}}$=2,方程无解.
综上,|AB|=4.
(II)设AB的方程为y=kx+b,
联立方程组$\left\{\begin{array}{l}{y=kx+b}\\{{y}^{2}=4x}\end{array}\right.$,消元得:k2x2+(2kb-4)x+b2=0,
∴x1+x2=$\frac{4-2kb}{{k}^{2}}$=2,∴b=$\frac{2}{k}-k$.∴x1x2=$\frac{{b}^{2}}{{k}^{2}}$=($\frac{2}{{k}^{2}}$-1)2.
∴|AB|=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$$\sqrt{4-4(\frac{2}{{k}^{2}}-1)^{2}}$=$\frac{4\sqrt{{k}^{4}-1}}{{k}^{2}}$.
∵y1+y2=k(x1+x2)+2b=2k+2b=$\frac{4}{k}$.∴AB的中点为C(1,$\frac{2}{k}$).
∴AB的中垂线方程为y-$\frac{2}{k}$=-$\frac{1}{k}$(x-1),即x+ky-3=0.
∴M(3,0).∴M到直线AB的距离d=|CM|=$\sqrt{(3-1)^{2}+\frac{4}{{k}^{2}}}$=$\frac{2\sqrt{1+{k}^{2}}}{|k|}$,
∵$\frac{|AB|}{d}$=$\sqrt{3}$,∴$\frac{4\sqrt{{k}^{4}-1}}{{k}^{2}}$=$\sqrt{3}$•$\frac{2\sqrt{1+{k}^{2}}}{|k|}$.即$\frac{2\sqrt{{k}^{2}-1}}{|k|}$=$\sqrt{3}$,
解得k=±2.
当k=2时,b=-1,当k=-2时,b=1.
∴AB的方程为y=2x-1或y=-2x+1.
点评 本题考查了抛物线的性质,直线与圆锥曲线的位置关系,弦长公式,属于中档题.


科目:高中数学 来源: 题型:解答题
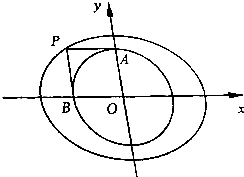 已知椭圆C1:$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{6}$=1,圆C2:x2+y2=4.过椭圆C1上点P作圆C2的两条切线,切点为A,B.
已知椭圆C1:$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{6}$=1,圆C2:x2+y2=4.过椭圆C1上点P作圆C2的两条切线,切点为A,B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 8 | C. | 12 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f({m}^{n})}{{m}^{n}}$ | B. | logmn•f(lognm) | C. | $\frac{f({n}^{m})}{{n}^{m}}$ | D. | lognm•f(logmn) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{8}{3}$ | C. | $\frac{7}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在斜四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为2$\sqrt{3}$的菱形,且∠BAD=$\frac{π}{3}$,若∠AA1C=$\frac{π}{2}$,且A1在底面ABCD上射影为△ABD的重心G.
如图,在斜四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为2$\sqrt{3}$的菱形,且∠BAD=$\frac{π}{3}$,若∠AA1C=$\frac{π}{2}$,且A1在底面ABCD上射影为△ABD的重心G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com