
分析 由题意、内角的范围、平方关系求出cosA和sinB的值,对A分类讨论后,分别由内角和定理、诱导公式、两角和的正弦函数求出sinC的值.
解答 解:在△ABC中,A,B,C∈(0,π),
∵$\left.\begin{array}{l}{sinA=\frac{5}{13},cosB=\frac{3}{5},}\end{array}\right.$
∴$\left.\begin{array}{l}{cosA=±\sqrt{1-si{n}^{2}A=}±\frac{12}{13}}\end{array}\right.$,$sinB=\sqrt{1-co{s}^{2}B}=\frac{4}{5}$,
①当$0<A<\frac{π}{2}$时,cosA=$\frac{12}{13}$,
所以$\left.\begin{array}{l}{sinC=sin[π-(A+B)]}\end{array}\right.$=sin(A+B)
=$\left.\begin{array}{l}{sinAcosB+cosAsinB}\end{array}\right.$
=$\left.\begin{array}{l}{\frac{5}{13}×\frac{3}{5}+\frac{12}{13}×\frac{4}{5}=\frac{63}{65}}\end{array}\right.$;
②当$\frac{π}{2}<A<π$时,cosA=-$\frac{12}{13}$,
所以sinC=sin(A+B)=$\left.\begin{array}{l}{sinAcosB+cosAsinB}\end{array}\right.$
=$\left.\begin{array}{l}{\frac{5}{13}×\frac{3}{5}-\frac{12}{13}×\frac{4}{5}=-\frac{33}{65}}\end{array}\right.$<0,舍去,
综上可得,sinC的值是$\frac{63}{65}$.
点评 本题考查两角和的正弦函数,诱导公式、平方关系,以及内角和定理的应用,注意内角的范围,考查化简、计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-32) | B. | (-∞,-27) | C. | (-32,-27) | D. | (-32,-27] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某高校调查了400名大学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25)[25,27.5),[27.5,30].根据此直方图,这400名大学生中每周的自习时间不少于25小时的人数是120.
某高校调查了400名大学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25)[25,27.5),[27.5,30].根据此直方图,这400名大学生中每周的自习时间不少于25小时的人数是120.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
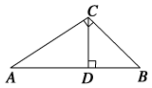
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}+\frac{i}{2}$ | B. | $\frac{1}{2}-\frac{i}{2}$ | C. | $-\frac{1}{2}+\frac{i}{2}$ | D. | $-\frac{1}{2}-\frac{i}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{19}{5}$ | B. | $\frac{19}{5}$ | C. | $\frac{11}{3}$ | D. | $-\frac{11}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com