在数列{an}中.已知a1=1.an+1=an+2(其中n∈N*).则a20=39．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

12．在数列{a_n}中，已知a₁=1，a_n+1=a_n+2（其中n∈N^*），则a₂₀=39．

分析根据a_n+1=a_n+2可得a_n+1-a_n=2，故数列{a_n}是以2 为公差的等差数列，再根据等差数列的通项公式即可求出a₂₀．

解答解：∵a_n+1=a_n+2，
∴a_n+1-a_n=2，
∴数列{a_n}是以2 为公差的等差数列．
∴a₂₀=a₁+（20-1）×2=39．
故答案为：39．

点评本题主要利用等差数列的通项公式求数列的项．解题的关键是要分析出数列{a_n}是以2为公差的等差数列，是基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

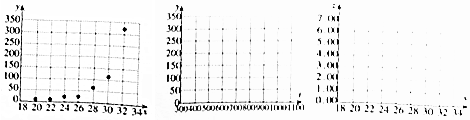
2．为了研究一种昆虫的产卵数y和温度x是否有关，现收集了7组观测数据列于下表中，并作出了散点图，发现样本点并没有分布在某个带状区域内，两个变量并不呈线性相关关系，现分别用模型①：y=C₁x²+C₂与模型②：y=e${\;}^{{C}_{3}x+{C}_{4}}$作为产卵数y和温度x的回归方程来建立两个变量之间的关系．

温度x/℃	20	22	24	26	28	30	32
产卵数y/个	6	10	21	24	64	113	322
t=x²	400	484	576	676	784	900	1024
Z=lny	1.79	2.30	3.04	3.18	4.16	4.73	5.77

$\overline{x}$	$\overline{t}$	$\overline{y}$	$\overline{z}$
26	692	80	3.57
$\frac{\sum_{i=1}^{7}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y）}}{\sum_{i=1}^{7}（{x}_{i}-\overline{x}）^{2}}$	$\frac{\sum_{i=1}^{7}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{7}（{t}_{i}-\overline{t}）^{2}}$	$\frac{\sum_{i=1}^{7}（{z}_{i}-\overline{z}）（{x}_{i}-\overline{x}）}{\sum_{i=1}^{7}（{x}_{i}-\overline{x}）^{2}}$	$\frac{\sum_{i=1}^{7}（{z}_{i}-\overline{z}）（{t}_{i}-\overline{t}）}{\sum_{i=1}^{7}（{t}_{i}-\overline{t}）^{2}}$
1157.54	0.43	0.32	0.00012

其中t_i=x_i²，$\overline{t}$=$\sum_{i=1}^{7}{t}_{i}$，z_i=lny_i，$\overline{u}$=$\sum_{i=1}^{7}{z}_{i}$，
附：对于一组数据（u₁，v₁），（u₂，v₂），…，（u_n，v_n），其回归直线v=βu+α的斜率和截距的最小二乘估计分别为：β=$\frac{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）（{v}_{i}-\overline{v}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）^{2}}$，α=$\overline{v}$-β$\overline{u}$．
（1）分别画出y关于t的散点图、z关于x的散点图，根据散点图判断哪一个模型更适宜作为回归方程类型？（给出判断即可，不必说明理由）．
（2）根据表中数据，分别建立两个模型下建立y关于x的回归方程；并在两个模型下分别估计温度为30℃时的产卵数．（C₁，C₂，C₃，C₄与估计值均精确到小数点后两位）（参考数据：e^4.65≈104.58，e^4.85≈127.74，e^5.05≈156.02）
（3）若模型①、②的相关指数计算分别为R₁²=0.82，R₂²=0.96，请根据相关指数判断哪个模型的拟合效果更好．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

3．设集合A={x|0≤x≤2}，B={x∈N|1≤x≤3}，则A∩B=（　　）

A．

{1，2}

B．

{1，2，3}

C．

{x|1≤x≤2}

D．

{x|0≤x≤3}

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

20．已知函数$f（x）=\sqrt{a{x^2}-2ax+1}$的定义域为R，则实数a的取值范围是[0，4]．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．已知函数$f（x）=\frac{1-x}{ax}+lnx$在（1，+∞）上是增函数，且a＞0．
（Ⅰ）求a的取值范围；
（Ⅱ）求函数g（x）=ln（1+x）-x在[0，+∞）上的最大值；
（Ⅲ）已知a＞1，b＞0，证明：$\frac{1}{a+b}≤ln\frac{a+b}{b}＜\frac{a}{b}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

17．设数列{a_n}是公比为q的等比数列，且|q|＞1．若数列{a_n}的连续四项构成集合{-72，-32，48，108}，则2q的值为-3．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．已知数列{a_n}中，a₁=1，a₂=3，其前n项和S_n满足S_n+1+S_n-1=2S_n+1，其中n≥2，n∈N^*．
（1）求证：数列{a_n}为等差数列，并求其通项公式；
（2）设b_n=$\frac{a_n}{2^n}\;，\;\;{T_n}$为数列{b_n}的前n项和，求T_n；
（3）设c_n=4ⁿ+（-1）_n-1λ•2^a_n（λ为非零整数，n∈N^*），试确定实数λ的值，使得对任意的n∈N^*，都有c_n+1＞c_n成立．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

1．在△ABC中，角A，B，C所对的边为a，b，c．已知c²=a²+b²-4bccosC，且A-C=$\frac{π}{2}$．
（Ⅰ）求cosC的值；
（Ⅱ）求cos（B+$\frac{π}{3}$）的值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．已知函数f（x）=x^m-$\frac{4}{x}$，且f（4）=3．
（1）求m的值；
（2）求f（x）的奇偶性．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学