
| �¶�x/�� | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| ������y/�� | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
| t=x2 | 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
| Z=lny | 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
| $\overline{x}$ | $\overline{t}$ | $\overline{y}$ | $\overline{z}$ |
| 26 | 692 | 80 | 3.57 |
| $\frac{\sum_{i=1}^{7}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y��}}{\sum_{i=1}^{7}��{x}_{i}-\overline{x}��^{2}}$ | $\frac{\sum_{i=1}^{7}��{t}_{i}-\overline{t}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{7}��{t}_{i}-\overline{t}��^{2}}$ | $\frac{\sum_{i=1}^{7}��{z}_{i}-\overline{z}����{x}_{i}-\overline{x}��}{\sum_{i=1}^{7}��{x}_{i}-\overline{x}��^{2}}$ | $\frac{\sum_{i=1}^{7}��{z}_{i}-\overline{z}����{t}_{i}-\overline{t}��}{\sum_{i=1}^{7}��{t}_{i}-\overline{t}��^{2}}$ |
| 1157.54 | 0.43 | 0.32 | 0.00012 |
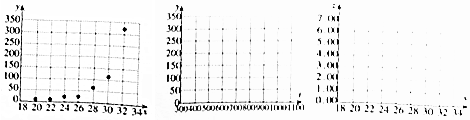
���� ��1������y����t��ɢ��ͼ��z����x��ɢ��ͼ�����ͼ���ж�ģ�͢ڸ�������Ϊ�ع鷽�����ͣ�
��2������ģ�͢ٵĻع�ϵ����д���ع鷽�̣����x=30ʱ$\stackrel{��}{y}$��ֵ��
����ģ�͢ڵĻع�ϵ����д���ع鷽�̣����x=30ʱ$\stackrel{��}{y}$��ֵ���ɣ�
��3������${{R}_{1}}^{2}$��${{R}_{2}}^{2}$�ж�ģ�͢ڵ����Ч�����ã�
��� �⣺��1������y����t��ɢ��ͼ��ͼ1��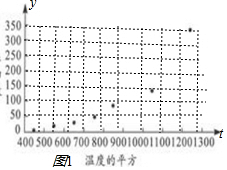
����z����x��ɢ��ͼ��ͼ2��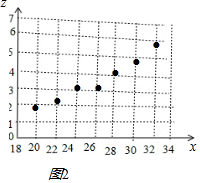
����ɢ��ͼ�����ж�ģ�͢ڸ�������Ϊ�ع鷽�����ͣ�
��2������ģ�͢٣���t=x2����y=C1x2+C2=C1t+C2��
����C1=$\frac{\sum_{i=1}^{7}{��t}_{i}-\overline{t}��{��y}_{i}-\overline{y}��}{{\sum_{i=1}^{7}{��t}_{i}-\overline{t}��}^{2}}$=0.43��
C2=$\overline{y}$-C1$\overline{t}$=80-0.43��692=-217.56��
������ع鷽��Ϊ$\stackrel{��}{y}$=0.43x2-217.56��
��x=30ʱ�������¶�Ϊ$\stackrel{��}{y}$=0.43��302-217.56=169.44��
����ģ�͢ڣ���y=${e}^{{C}_{1}x{+C}_{2}}$��
��z=lny=C3x+C4��
����C3=$\frac{\sum_{i=1}^{7}{��z}_{i}-\overline{z}��{��x}_{i}-\overline{x}��}{{\sum_{i=1}^{7}{��x}_{i}-\overline{x}��}^{2}}$=0.32��
C4=$\overline{z}$-C3$\overline{x}$=3.57-0.32��26=-4.75��
������ع鷽��Ϊ$\stackrel{��}{z}$=0.32x-4.75��
��$\stackrel{��}{y}$=e0.32x-4.75��
��x=30ʱ�������¶�Ϊ$\stackrel{��}{y}$=e0.32��30-4.75��127.74��
��3����R12=0.82��R22=0.96��
��${{R}_{1}}^{2}$��${{R}_{2}}^{2}$��
��ģ�͢ڵ����Ч�����ã�
���� ���⿼����ɢ��ͼ�Լ��ع鷽�̺����ָ����Ӧ�����⣬Ҳ�����˷������ж�������Ӧ�����⣬���ۺ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
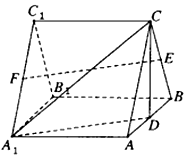 ��ͼ��������ABC-A1B1C1�У����ⳤ����ȣ�D��E��F�ֱ�Ϊ��AB��BC��A1C1���е㣮
��ͼ��������ABC-A1B1C1�У����ⳤ����ȣ�D��E��F�ֱ�Ϊ��AB��BC��A1C1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�1�� | B�� | ��1��+�ޣ� | C�� | ��e��+�ޣ� | D�� | [1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{5}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{3}{4}$ | D�� | $\frac{5}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com