
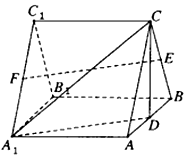
 如图,三棱柱ABC-A1B1C1中,各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.分析 (I)连接DE,通过证明四边形A1DEF是平行四边形得出EF∥A1D,从而EF∥平面A1CD;
(II)过B作BM⊥A1D交延长线于M,连接CM,则可证BM⊥平面A1CD,即∠BCM为所求线面角,设三棱柱棱长为1,利用三角形相似求出BM即可得出sin∠BCM=$\frac{BM}{BC}$.
解答 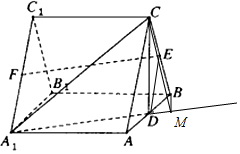 证明:(I)连接DE,
证明:(I)连接DE,
∵D,E分别是AB,BC的中点,
∴DE$\stackrel{∥}{=}$$\frac{1}{2}$AC,
∵F是A1C1的中点,∴A1F=$\frac{1}{2}$A1C1,
又AC$\stackrel{∥}{=}$A1C1,
∴A1F$\stackrel{∥}{=}$DE,
∴四边形A1DEF是平行四边形,
∴EF∥A1D,又EF?平面A1CD,A1D?平面A1CD,
∴EF∥平面A1CD.
(II)过B作BM⊥A1D交延长线于M,连接CM,
∵ABC是等边三角形,∴CD⊥AB,
又A1A⊥平面ABC,CD?平面ABC,
∴A1A⊥CD,
∴CD⊥平面ABCD,又BM?平面ABCD,
∴CD⊥BM,又CD?平面A1CD,A1D?平面A1CD,CD∩A1D=D,
∴BM⊥平面A1CD,
∴∠BCM为直线BC与平面A1CD所成的角,
设直三棱柱棱长为1,则BM=$\frac{\sqrt{5}}{5}$,
∴sin∠BCM=$\frac{BM}{BC}$=$\frac{\sqrt{5}}{5}$.
点评 本题考查了线面平行的判定,线面角的计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
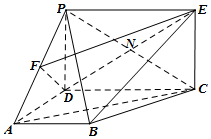 如图,PD垂直于梯形ABCD所在的平面,∠ADC=∠BAD=90°.F为PA中点,PD=$\sqrt{2}$,AB=AD=$\frac{1}{2}$CD=1. 四边形PDCE为矩形,线段PC交DE于点N.
如图,PD垂直于梯形ABCD所在的平面,∠ADC=∠BAD=90°.F为PA中点,PD=$\sqrt{2}$,AB=AD=$\frac{1}{2}$CD=1. 四边形PDCE为矩形,线段PC交DE于点N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
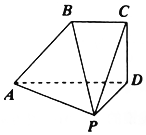 如图,五面体PABCD中,CD⊥平面PAD,ABCD为直角梯形,∠BCD=$\frac{π}{2}$,PD=BC=CD=$\frac{1}{2}$AD,AP⊥PD.
如图,五面体PABCD中,CD⊥平面PAD,ABCD为直角梯形,∠BCD=$\frac{π}{2}$,PD=BC=CD=$\frac{1}{2}$AD,AP⊥PD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
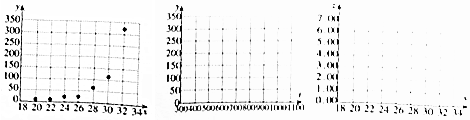
| 温度x/℃ | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| 产卵数y/个 | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
| t=x2 | 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
| Z=lny | 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
| $\overline{x}$ | $\overline{t}$ | $\overline{y}$ | $\overline{z}$ |
| 26 | 692 | 80 | 3.57 |
| $\frac{\sum_{i=1}^{7}({x}_{i}-\overline{x})({y}_{i}-\overline{y)}}{\sum_{i=1}^{7}({x}_{i}-\overline{x})^{2}}$ | $\frac{\sum_{i=1}^{7}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{7}({t}_{i}-\overline{t})^{2}}$ | $\frac{\sum_{i=1}^{7}({z}_{i}-\overline{z})({x}_{i}-\overline{x})}{\sum_{i=1}^{7}({x}_{i}-\overline{x})^{2}}$ | $\frac{\sum_{i=1}^{7}({z}_{i}-\overline{z})({t}_{i}-\overline{t})}{\sum_{i=1}^{7}({t}_{i}-\overline{t})^{2}}$ |
| 1157.54 | 0.43 | 0.32 | 0.00012 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {1,2,3} | C. | {x|1≤x≤2} | D. | {x|0≤x≤3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com