
分析 由f'(x)=6x2-6,x>t,知x>t时,f(x)=2x3-6x一定存在单调递增区间,从而要使无论t取何值,函数f(x)在区间(-∞,+∞)总是不单调,必须有f(x)=(4a-3)x+2a-4不能为增函数,由此能求出a的取值范围.
解答 解:对于函数f(x)=2x3-6x,
f'(x)=6x2-6,x>t
当6x2-6>0时,即x>1或x<-1,
此时f(x)=2x3-6x,为增函数
当6x2-6<0时,-1<x<1,
∵x>t,∴f(x)=2x3-6x一定存在单调递增区间
要使无论t取何值,
函数f(x)在区间(-∞,+∞)总是不单调
∴f(x)=(4a-3)x+2a-4不能为增函数
∴4a-3≤0,∴a≤$\frac{3}{4}$.
故a的取值范围是(-∞,$\frac{3}{4}$].
故答案为:(-∞,$\frac{3}{4}$].
点评 本题考查实数的取值范围的求法,考查推理论证能力、运算求解能力、空间想象能力,考查等价转化思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
| 平均气温x(℃) | 9 | 10 | 12 | 11 | 8 |
| 销量y(杯) | 23 | 25 | 30 | 26 | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
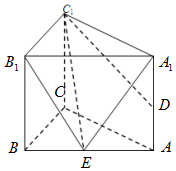 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是AA1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{13}{6}$,$\frac{7}{2}$] | B. | ($\frac{7}{2}$,$\frac{25}{6}$] | C. | ($\frac{25}{6}$,$\frac{11}{2}$] | D. | ($\frac{11}{2}$,$\frac{37}{6}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
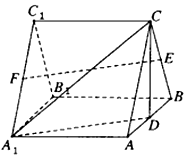 如图,三棱柱ABC-A1B1C1中,各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com