
分析 首先根据线性规划问题和基本不等式求出函数的最值,再利用正弦型函数的最小正周期,求出结果.
解答 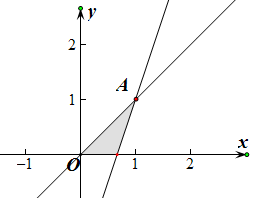 解:设x、y的线性约束条件$\left\{\begin{array}{l}{x-y≥0}\\{3x-y-2≤0}\\{x≥0,y≥0}\end{array}\right.$,如图所示:
解:设x、y的线性约束条件$\left\{\begin{array}{l}{x-y≥0}\\{3x-y-2≤0}\\{x≥0,y≥0}\end{array}\right.$,如图所示:
解得A(1,1)目标函数z=ax+by(a>0,b>0)的最大值为2,
即:a+b=2,
所以:$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$≥2,
则y=sin(2x+$\frac{π}{3}$)的最小正周期为π,
故答案为:π.
点评 本题考查的知识要点:线性规划问题,基本不等式的应用,正弦型函数的最小正周期,属于基础题型.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
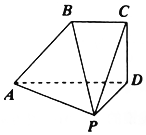 如图,五面体PABCD中,CD⊥平面PAD,ABCD为直角梯形,∠BCD=$\frac{π}{2}$,PD=BC=CD=$\frac{1}{2}$AD,AP⊥PD.
如图,五面体PABCD中,CD⊥平面PAD,ABCD为直角梯形,∠BCD=$\frac{π}{2}$,PD=BC=CD=$\frac{1}{2}$AD,AP⊥PD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 温度x/℃ | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| 产卵数y/个 | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
| t=x2 | 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
| Z=lny | 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
| $\overline{x}$ | $\overline{t}$ | $\overline{y}$ | $\overline{z}$ |
| 26 | 692 | 80 | 3.57 |
| $\frac{\sum_{i=1}^{7}({x}_{i}-\overline{x})({y}_{i}-\overline{y)}}{\sum_{i=1}^{7}({x}_{i}-\overline{x})^{2}}$ | $\frac{\sum_{i=1}^{7}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{7}({t}_{i}-\overline{t})^{2}}$ | $\frac{\sum_{i=1}^{7}({z}_{i}-\overline{z})({x}_{i}-\overline{x})}{\sum_{i=1}^{7}({x}_{i}-\overline{x})^{2}}$ | $\frac{\sum_{i=1}^{7}({z}_{i}-\overline{z})({t}_{i}-\overline{t})}{\sum_{i=1}^{7}({t}_{i}-\overline{t})^{2}}$ |
| 1157.54 | 0.43 | 0.32 | 0.00012 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
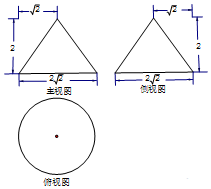 某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为( )
某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $2-\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com