Question

14．三棱锥P-ABC的四个顶点都在球D的表面上，PA⊥平面ABC，AB⊥BC，PA=3，AB=BC=2，则球O的表面积为（　　）

• A． 13π
• B． 17π
• C． 52π
• D． 68π

Answer 1

分析 取PC的中点O，连结OA、OB．由线面垂直的判定与性质，证出BC⊥PB且PA⊥AC，得到△PAC与△PBC是具有公共斜边的直角三角形，从而得出OA=OB=OC=OP=$\frac{1}{2}$PC，所以P、A、B、C四点在以O为球心的球面上．根据题中的数据，利用勾股定理算出PC长，进而得到球半径R，利用球的表面积公式加以计算，可得答案．

解答 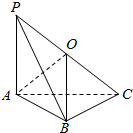解：取PC的中点O，连结OA、OB
∵PA⊥平面ABC，BC?平面ABC，∴PA⊥BC，
又∵AB⊥BC，PA∩AB=A，∴BC⊥平面PAB，
∵PB?平面PAB，∴BC⊥PB，
∵OB是Rt△PBC的斜边上的中线，OB=$\frac{1}{2}$PC．
同理可得：Rt△PAC中，OA=$\frac{1}{2}$PC，
∴OA=OB=OC=OP=$\frac{1}{2}$PC，可得P、A、B、C四点在以O为球心的球面上．
Rt△ABC中，AB=BC=2，可得AC=2$\sqrt{2}$，
Rt△PAC中，PA=3，可得PC=$\sqrt{17}$．
∴球O的半径R=$\frac{\sqrt{17}}{2}$，可得球O的表面积为S=4πR²=17π．
故选：B．

点评 本题给出特殊的三棱锥，由它的外接球的表面积．着重考查了线面垂直的判定与性质、勾股定理与球的表面积公式等知识，属于中档题．