
分析 (1)利用函数的单调性的定义,即可得出结论;
(2)利用f(x)是奇函数,则f(x)+f(-x)=0,即可求出a.
解答 解:(1)设x1<x2,
则f(x1)-f(x2)=$\frac{a}{2}$-$\frac{{2}^{{x}_{1}}}{{2}^{{x}_{1}+1}}$-$\frac{a}{2}$+$\frac{{2}^{{x}_{2}}}{{2}^{{x}_{2}}+1}$=$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$.
∵x1<x2,∴${2}^{{x}_{1}}$<${2}^{{x}_{2}}$,即${2}^{{x}_{1}}$-${2}^{{x}_{2}}$>0.
又${2}^{{x}_{1}}$+1>0,${2}^{{x}_{2}}$+1>0.
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴函数f(x)在定义域上是减函数.--------------------(6分)
(2)假设f(x)是奇函数,则f(x)+f(-x)=0.
即$\frac{a}{2}$-$\frac{{2}^{x}}{{2}^{x}+1}$+$\frac{a}{2}$-$\frac{{2}^{-x}}{{2}^{-x}+1}$=a-1=0,∴a=1.
∴存在实数a=1,使f(x)是奇函数.--------------------(12分)
点评 本题考查函数的单调性、奇偶性,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-$\frac{1}{2}$<x≤0} | B. | {x|-$\frac{1}{2}$<x≤0或1≤x<2} | C. | {x|-1<x≤0} | D. | {x|-1<x≤0或1≤x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在一条直线l、l⊥α、l⊥β | B. | 存在一个面r、r∥α、r∥β | ||
| C. | 存在一个平面r、r⊥α、r⊥β | D. | 存在一条直线l、l⊥α、l∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
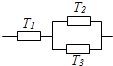 三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )
三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )| A. | $\frac{7}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{15}{32}$ | D. | $\frac{17}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=g(x)的图象关于直线$x=-\frac{π}{3}$对称 | B. | y=g(x)图象关于原点对称 | ||
| C. | y=g(x)的图象关于点$({-\frac{π}{3},0})$对称 | D. | y=g(x)图象关于y轴对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13π | B. | 17π | C. | 52π | D. | 68π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com