练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．若正四棱锥P-ABCD的棱长都为2，且五个顶点P、A、B、C、D同在一个球上，则球的表面积为8π．

    分析 画出图形，正四棱锥P-ABCD的底面是正方形，推出底面中心到顶点的距离为球的半径，求出球的表面积．

    解答 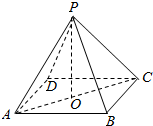解：正四棱锥P-ABCD的底面是正方形，对角线的长为2$\sqrt{2}$，如图，
    因为P-ABCD是所有棱长均为2的正四棱锥，所以△PAC与△DPB都是等腰直角三角形，中心到P，到A，B，C，D的距离相等，是外接球的半径R，R2+（$\sqrt{2}$）2=22，解得R=$\sqrt{2}$，
    ∴球的表面积S=4π（$\sqrt{2}$）2=8π．
    故答案为：8π．

    点评 本题给出正四棱锥的形状，求它的外接球的表面积，着重考查了正棱锥的性质、多面体的外接球、勾股定理与球的表面积公式等知识，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    1．函数f（x）=log2（-4x+5）的单调性是减函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知f（x）=3ax-2a+1在区间（-1，1）内存在x0，使f（x0）=0，则实数a的取值范围是（　　）
    A．$（-1，\frac{1}{5}）$B．$（-\frac{1}{5}，+∞）$C．$（-∞，-1）∪（\frac{1}{5}，+∞）$D．（-∞，-1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．对于函数f（x）=$\frac{a}{2}$-$\frac{{2}^{x}}{{2}^{x}+1}$（a∈R）．
    （1）探讨函数f（x）的单调性；
    （2）是否存在实数a，使函数f（x）为奇函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．在数列{an}中，a1=1，Sn为数列{an}的前n项和，当n≥2时，${a_n}，{S_n}，{S_n}-\frac{1}{2}$成等比数列，则an=$\left\{\begin{array}{l}{1，n=1}\\{\frac{1}{2n-1}-\frac{1}{2n-3}，n≥2}\end{array}\right.$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．对于向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$和实数λ，下列正确的是（　　）
    A．若$\overrightarrow{a}$•$\overrightarrow{b}$=0，则$\overrightarrow{a}$=0或$\overrightarrow{b}$=0B．若λ$\overrightarrow{a}$=0，则λ=0或$\overrightarrow{a}$=$\overrightarrow{0}$
    C．若$\overrightarrow{a}$2=$\overrightarrow{b}$2，则$\overrightarrow{a}$=$\overrightarrow{b}$或$\overrightarrow{a}$=-$\overrightarrow{b}$D．若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$，则$\overrightarrow{b}$=$\overrightarrow{c}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知角α的终边经过点（-2，1），则cos2α=（　　）
    A．-$\frac{3}{5}$B．$\frac{3}{5}$C．$\frac{2}{5}$D．-$\frac{2}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．若存在实数m，n，使得$\left\{\begin{array}{l}{\frac{1}{{e}^{x}}-\frac{a}{x}≥0}\\{x＞0}\end{array}\right.$的解集为[m，n]，则a的取值范围为（　　）
    A．（$\frac{1}{{e}^{x}}$，e）B．（0，$\frac{1}{{e}^{x}}$）C．（0，$\frac{1}{2e}$）D．（0，$\frac{1}{e}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知定义在R上的函数f（x）=|2x-2|+1，g（x）=x2+2x-$\frac{1}{2}$．
    （1）解不等式f（x）≥3-x；
    （2）若对?x∈R，$\frac{1}{2}$f（x）+|x+1|＞g（m）恒成立，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案